Question

Consider the reaction $A \longrightarrow B$, graph between half-life $(t_{1/2})$ and initial concentration (a) of the reaction is:

Hence graph between $-\frac{d[A]}{dt}$ and time will be:

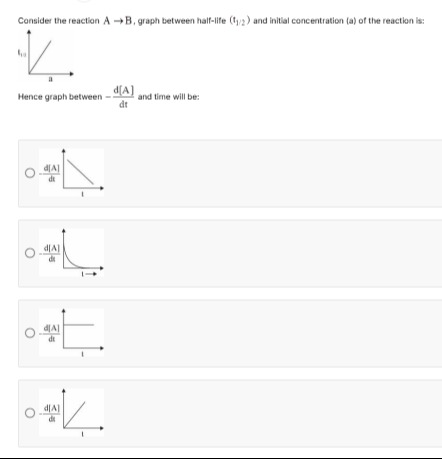
• A. Option 1 shows a linearly decreasing rate.
• B. Option 2 shows an exponentially decreasing rate.
• C. Option 3 shows a constant rate (horizontal line).
• D. Option 4 shows a linearly increasing rate.

Answer 1

Answer: (C)

Option 3

Answer 2

The initial graph shows that the half-life ($t_{1/2}$) is directly proportional to the initial concentration (a). This relationship ($t_{1/2} \propto a$) is characteristic of a zero-order reaction. For a zero-order reaction, the rate law is given by Rate $= -\frac{d[A]}{dt} = k[A]^0 = k$. This implies that the rate of the reaction is constant and does not change with time. Therefore, the graph of $-\frac{d[A]}{dt}$ versus time will be a horizontal straight line.