Solveeit Logo
Login

Question

Question: Consider the ray diagram for the refraction given below. The maximum value of angle 6 for which th...

Consider the ray diagram for the refraction given below. The maximum value of
angle 6 for which the light suffers total internal reflection at the vertical surface, is

A. cos⁡−1(34)\cos ^{-1}\left(\dfrac{3}{4}\right)
B. sin⁡−1(34){{\sin }^{-1}}\left( \dfrac{3}{4} \right)
C. tan⁡−1(34){{\tan }^{-1}}\left( \dfrac{3}{4} \right)
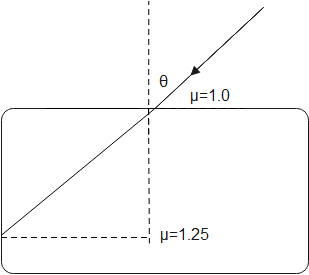
D. cos⁡−1(43)\cos ^{-1}\left(\dfrac{4}{3}\right)

Explanation

Solution

If light passes from the optically denser to the rare medium, the light is partially reflected back into the denser medium at the interface and partially refracted back into the rare medium at the interface. Total internal reflection is called this type of reflection. During the refraction, the light ray bends away from normal when light travels from denser medium to rarer medium at the interface.

Complete Step-by-Step solution:
A portion of light is reflected back to a denser medium when light passes from a denser medium to a rarer medium and a portion of light is refracted to a rarer medium. Internal reflection is called this phenomenon. Under certain conditions, it is possible to reflect the whole of the incident light back to the denser medium.

For total internal reflection to occur at the vertical surface, the minimum angle the ray incident on vertical surface can make is sin⁡−1(11.25)=sin⁡−1(45)\sin ^{-1}\left(\dfrac{1}{1.25}\right)=\sin ^{-1}\left(\dfrac{4}{5}\right)

Hence, the maximum angle that the refracted ray at the horizontal surface makes with the vertical =90∘−sin⁡−1(45)=90^{\circ}-\sin ^{-1}\left(\dfrac{4}{5}\right)

Hence, from Snell's law for reflection at horizontal surface,
sin⁡θmax⁡ =1.25×sin⁡(90∘−sin⁡−1(45)))\sin {{\theta }_{\max }}\text{ }\left. =1.25\times \sin \left( {{90}^{{}^\circ }}-{{\sin }^{-1}}\left( \dfrac{4}{5} \right) \right) \right)
sin⁡θmax⁡=1.25×sin⁡(90∘−sin⁡−1(45))) =1.25×cos⁡(sin⁡−1(45)) =34 ⟹θmax⁡=sin⁡−1(34).\begin{aligned} \sin \theta_{\max } &\left.=1.25 \times \sin \left(90^{\circ}-\sin ^{-1}\left(\dfrac{4}{5}\right)\right)\right) \\\ &=1.25 \times \cos \left(\sin ^{-1}\left(\dfrac{4}{5}\right)\right) \\\ &=\dfrac{3}{4} \\\ \Longrightarrow \theta_{\max } &=\sin ^{-1}\left(\dfrac{3}{4}\right) \end{aligned} .
∴θmax⁡=sin⁡−1(34)\therefore {{\theta }_{\max }}={{\sin }^{-1}}\left( \dfrac{3}{4} \right)

The maximum value of angle 6 for which the light suffers total internal reflection at the vertical surface, is sin⁡−1(34){{\sin }^{-1}}\left( \dfrac{3}{4} \right)

Hence, the correct option is (B).

Note:
Total internal reflection only occurs when the ray of light is travelling from denser medium to rarer medium i.e. total internal reflection does not occur when the ray travelling from rarer to denser medium. For total internal reflection to occur the angle of incidence must be greater than the critical angle.