Solveeit Logo
Login

Question

Question: Consider the ray diagram for the refraction given. The maximum value of angle \(\theta\) for which t...

Consider the ray diagram for the refraction given. The maximum value of angle θ\theta for which the light suffers total internal reflection at the vertical surface, is?

A. cos⁡−134{\cos}^{-1} \dfrac {3}{4}
B. sin⁡−134{\sin}^{-1} \dfrac {3}{4}
C. tan⁡−143{\tan}^{-1} \dfrac {4}{3}
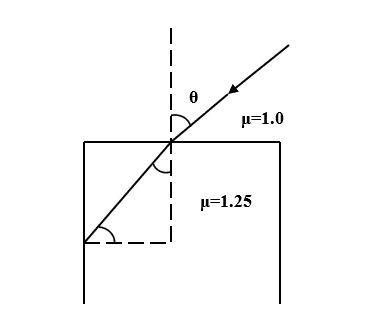
D. cos⁡−143{\cos}^{-1} \dfrac {4}{3}

Explanation

Solution

To solve this problem, first find the critical angle at the vertical surface. Then, find the maximum angle that the refracted ray at the horizontal surface makes with the vertical surface. This can be calculated by subtracting the critical angle from 90°. Then, use the formula for Snell’s law. Substitute the values and calculate the value of θ\theta. This will be the maximum value of angle θ\theta for which the light suffers total internal reflection at the vertical surface.
Formula used:
sin⁡θc=μ1μ2\sin{{\theta}_{c}}= \dfrac {{\mu}_{1}}{{\mu}_{2}}
μ2=sin⁡θmaxsin⁡θr{\mu}_{2}= \dfrac {\sin {{\theta}_{max}}}{\sin {{\theta}_{r}}}

Complete answer:

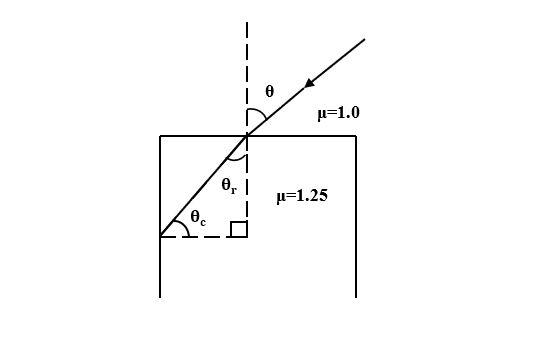
Given: μ1{\mu}_{1}= 1.0
μ2{\mu}_{2}= 1.25
For total internal reflection to occur at the vertical surface, the formula for critical angle is given by,
sin⁡θc=μ1μ2\sin{{\theta}_{c}}= \dfrac {{\mu}_{1}}{{\mu}_{2}}
Substituting the values in above equation we get,
sin⁡θc=1.01.25\sin {{\theta}_{c}}= \dfrac {1.0}{1.25}
⇒θc=sin⁡−111.25\Rightarrow {\theta}_{c} = {\sin}^{-1} \dfrac {1}{1.25}
⇒θc=53.13°\Rightarrow {\theta}_{c} =53.13°
The maximum angle that the refracted ray at the horizontal surface makes with the vertical surface is given by,
θr=90°−θc{\theta}_{r}= 90°- {\theta}_{c}
Substituting the value of θ\theta in above equation we get,
θr=90°−53.13°{\theta}_{r}= 90°- 53.13°
⇒θr=36.87°\Rightarrow{\theta}_{r}=36.87°
From Snell’s law we know,
μ2=sin⁡θmaxsin⁡θr{\mu}_{2}= \dfrac {\sin {{\theta}_{max}}}{\sin {{\theta}_{r}}}
Substituting values in above equation we get,
1.25=sin⁡θmaxsin⁡36.87°1.25= \dfrac {\sin {{\theta}_{max}}}{\sin {36.87°}}
⇒1.25=sin⁡θmax0.60\Rightarrow 1.25= \dfrac {\sin {{\theta}_{max}}}{0.60}
⇒sin⁡θmax=1.25×0.60\Rightarrow \sin {{\theta}_{max}}= 1.25 \times 0.60
⇒sin⁡θmax=0.75\Rightarrow \sin {{\theta}_{max}}= 0.75
⇒sin⁡θmax=34\Rightarrow \sin {{\theta}_{max}}= \dfrac {3}{4}
⇒θmax=sin⁡−134\Rightarrow {\theta}_{max} = {\sin}^{-1} \dfrac {3}{4}
Hence, the maximum value of angle θ\theta for which the light suffers total internal reflection at the vertical surface, is sin⁡−134{\sin}^{-1} \dfrac {3}{4}.

So, the correct answer is option B i.e. sin⁡−134{\sin}^{-1} \dfrac {3}{4}.

Note:
Students must remember that there are few requirements for total internal reflection which are mentioned below:
1. The incident light should be travelling in a more optically denser medium and approaching a medium which is less dense. Water is optically denser as compared to air which is a rarer medium.
2. The angle of incidence should always be greater than the critical angle.