Question

Consider the planes $P_1, P_2$ and points $A(2,5,1)$ and $B(1,3,0)$ where

$P_1: x+y+z=3$

$P_2: 2x+y-z=4$

Then identify the correct statement(s)

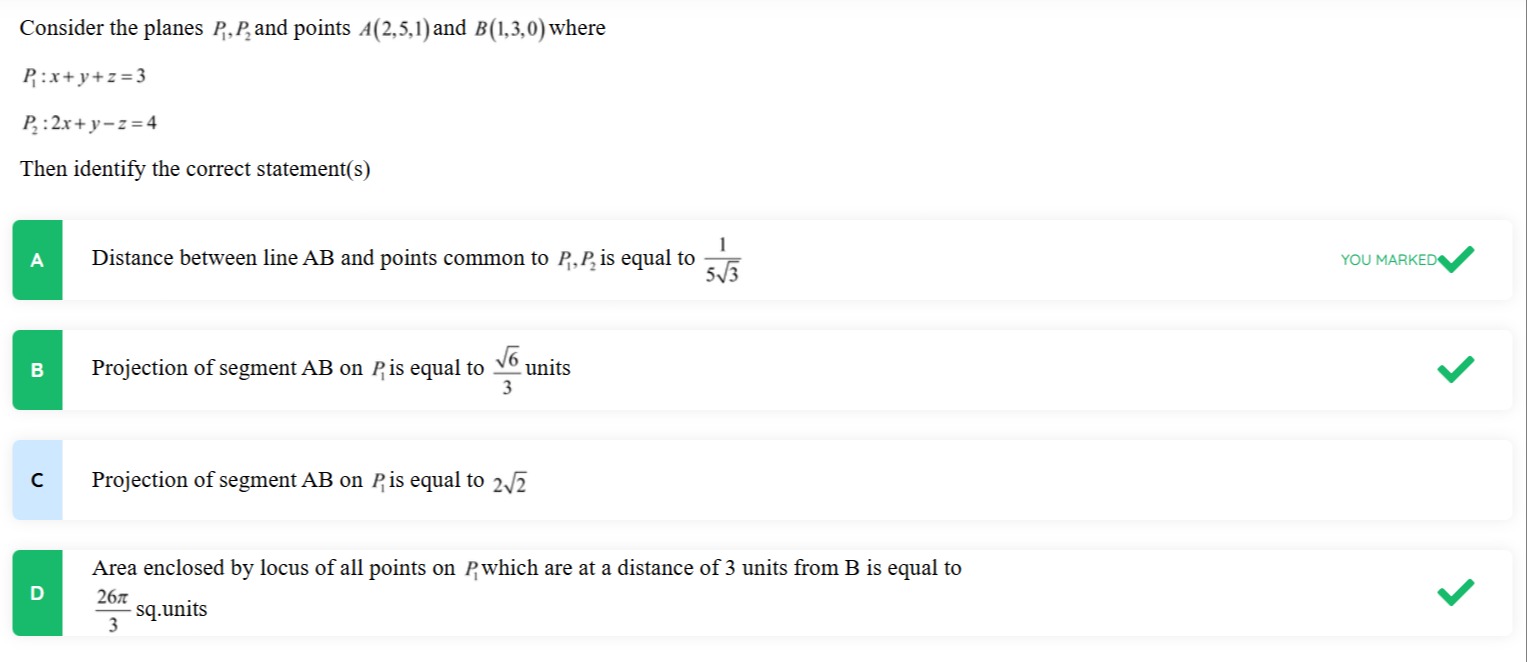
• A. Distance between line AB and points common to $P_1, P_2$ is equal to $\frac{1}{5\sqrt{3}}$
• B. Projection of segment AB on $P_1$ is equal to $\frac{\sqrt{6}}{3}$ units
• C. Projection of segment AB on $P_1$ is equal to $2\sqrt{2}$
• D. Area enclosed by locus of all points on $P_1$ which are at a distance of 3 units from B is equal to $\frac{26\pi}{3}$ sq.units

Answer 1

Answer: (A), (B), (D)

A, B, D

Answer 2

The problem asks us to evaluate four statements regarding two planes $P_1: x+y+z=3$, $P_2: 2x+y-z=4$ and two points $A(2,5,1)$, $B(1,3,0)$.

Statement A: Distance between line AB and points common to $P_1, P_2$.

The points common to $P_1$ and $P_2$ form a line, which is the intersection of the two planes. The normal vectors are $\vec{n_1}=(1,1,1)$ and $\vec{n_2}=(2,1,-1)$. The direction vector of the intersection line L is $\vec{v_L} = \vec{n_1} \times \vec{n_2} = (-2,3,-1)$.

To find a point on L, we solve $x+y+z=3$ and $2x+y-z=4$. Adding the equations gives $3x+2y=7$. Let $y=2$, then $3x=3$, $x=1$. Substituting into $x+y+z=3$, $1+2+z=3$, so $z=0$. Thus, $C(1,2,0)$ is a point on L. The line L can be represented as $\vec{r}_L(t) = (1,2,0) + t(-2,3,-1)$.

The line AB passes through $A(2,5,1)$ and has direction vector $\vec{v_{AB}} = B-A = (1-2, 3-5, 0-1) = (-1,-2,-1)$. The line AB can be represented as $\vec{r}_{AB}(s) = (2,5,1) + s(-1,-2,-1)$.

The distance between two skew lines $\vec{r}_1 = \vec{a_1} + t \vec{v_1}$ and $\vec{r}_2 = \vec{a_2} + s \vec{v_2}$ is $d = \frac{|(\vec{a_2} - \vec{a_1}) \cdot (\vec{v_1} \times \vec{v_2})|}{||\vec{v_1} \times \vec{v_2}||}$.

Here, $\vec{a_1}=C(1,2,0)$, $\vec{v_1}=\vec{v_L}=(-2,3,-1)$, $\vec{a_2}=A(2,5,1)$, $\vec{v_2}=\vec{v_{AB}}=(-1,-2,-1)$.

$\vec{a_2}-\vec{a_1} = (2-1, 5-2, 1-0) = (1,3,1)$.

$\vec{v_1} \times \vec{v_2} = (-2,3,-1) \times (-1,-2,-1) = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ -2 & 3 & -1 \\ -1 & -2 & -1 \end{vmatrix} = \mathbf{i}(-3-2) - \mathbf{j}(2-1) + \mathbf{k}(4+3) = (-5,-1,7)$.

$||\vec{v_1} \times \vec{v_2}|| = \sqrt{(-5)^2+(-1)^2+7^2} = \sqrt{25+1+49} = \sqrt{75} = 5\sqrt{3}$.

$(\vec{a_2}-\vec{a_1}) \cdot (\vec{v_1} \times \vec{v_2}) = (1,3,1) \cdot (-5,-1,7) = 1(-5)+3(-1)+1(7) = -5-3+7 = -1$.

The distance is $d = \frac{|-1|}{5\sqrt{3}} = \frac{1}{5\sqrt{3}}$. Statement A is correct.

Statement B and C: Projection of segment AB on $P_1$.

The length of the projection of segment AB on plane $P_1$ is $||\vec{AB}|| \cos \theta$, where $\theta$ is the angle between $\vec{AB}$ and $P_1$. The angle between vector $\vec{v}$ and plane with normal $\vec{n}$ satisfies $\sin \theta = \frac{|\vec{v} \cdot \vec{n}|}{||\vec{v}|| ||\vec{n}||}$.

$\vec{AB} = (-1,-2,-1)$, $||\vec{AB}|| = \sqrt{(-1)^2+(-2)^2+(-1)^2} = \sqrt{6}$.

Normal to $P_1$ is $\vec{n_1}=(1,1,1)$, $||\vec{n_1}|| = \sqrt{1^2+1^2+1^2} = \sqrt{3}$.

$\vec{AB} \cdot \vec{n_1} = (-1)(1)+(-2)(1)+(-1)(1) = -4$.

$\sin \theta = \frac{|-4|}{\sqrt{6}\sqrt{3}} = \frac{4}{\sqrt{18}} = \frac{4}{3\sqrt{2}} = \frac{2\sqrt{2}}{3}$.

$\cos^2 \theta = 1 - \sin^2 \theta = 1 - (\frac{2\sqrt{2}}{3})^2 = 1 - \frac{8}{9} = \frac{1}{9}$. Since $0 \le \theta \le 90^\circ$, $\cos \theta = \sqrt{\frac{1}{9}} = \frac{1}{3}$.

Length of projection $= ||\vec{AB}|| \cos \theta = \sqrt{6} \cdot \frac{1}{3} = \frac{\sqrt{6}}{3}$.

Statement B is correct, and Statement C is incorrect.

Statement D: Area enclosed by locus of all points on $P_1$ which are at a distance of 3 units from B.

The locus of points at a distance of 3 units from B is a sphere centered at $B(1,3,0)$ with radius $R=3$. The equation is $(x-1)^2+(y-3)^2+z^2=9$.

The locus of points on $P_1$ at a distance of 3 units from B is the intersection of this sphere and the plane $P_1: x+y+z=3$.

The intersection is a circle if the distance from the center of the sphere B to the plane $P_1$ is less than the radius R.

Distance from $B(1,3,0)$ to $P_1: x+y+z-3=0$ is $d = \frac{|1(1)+1(3)+1(0)-3|}{\sqrt{1^2+1^2+1^2}} = \frac{|1+3-3|}{\sqrt{3}} = \frac{1}{\sqrt{3}}$.

Since $d = \frac{1}{\sqrt{3}} < R=3$, the intersection is a circle.

The radius of this circle, r, is given by $r^2 = R^2 - d^2 = 3^2 - (\frac{1}{\sqrt{3}})^2 = 9 - \frac{1}{3} = \frac{27-1}{3} = \frac{26}{3}$.

The radius of the circle is $r = \sqrt{\frac{26}{3}}$.

The area enclosed by this circle is $Area = \pi r^2 = \pi (\frac{26}{3}) = \frac{26\pi}{3}$.

Statement D is correct.

The correct statements are A, B, and D.