Question

Consider the parabola whose focus is at $\left( 0,0 \right)$ and the tangent at the vertex is $x-y+1=0$. Tangent drawn to the parabola at the extremities of the chord $3x+2y=0$ intersect at an angle
(a) $\dfrac{\pi }{6}$
(b) $\dfrac{\pi }{3}$
(c) $\dfrac{\pi }{2}$
(d) none

Answer 1

We start solving the problem by substituting the point $\left( 0,0 \right)$ in the equation of chord $3x+2y=0$ which tells us that this point lies on the given chord. We then recall the fact that the chord of the parabola which passes through the focus in a parabola is known as focal chord and the tangents at the ends of the focal chord in a parabola intersects at right angles which gives us the required answer.

Complete step by step answer:
According to the problem, we are given that the focus of the parabola is $\left( 0,0 \right)$ and the tangent at the vertex is $x-y+1=0$. We need to find the angle of intersection of the tangents drawn to the parabola at the extremities of the chord $3x+2y=0$.

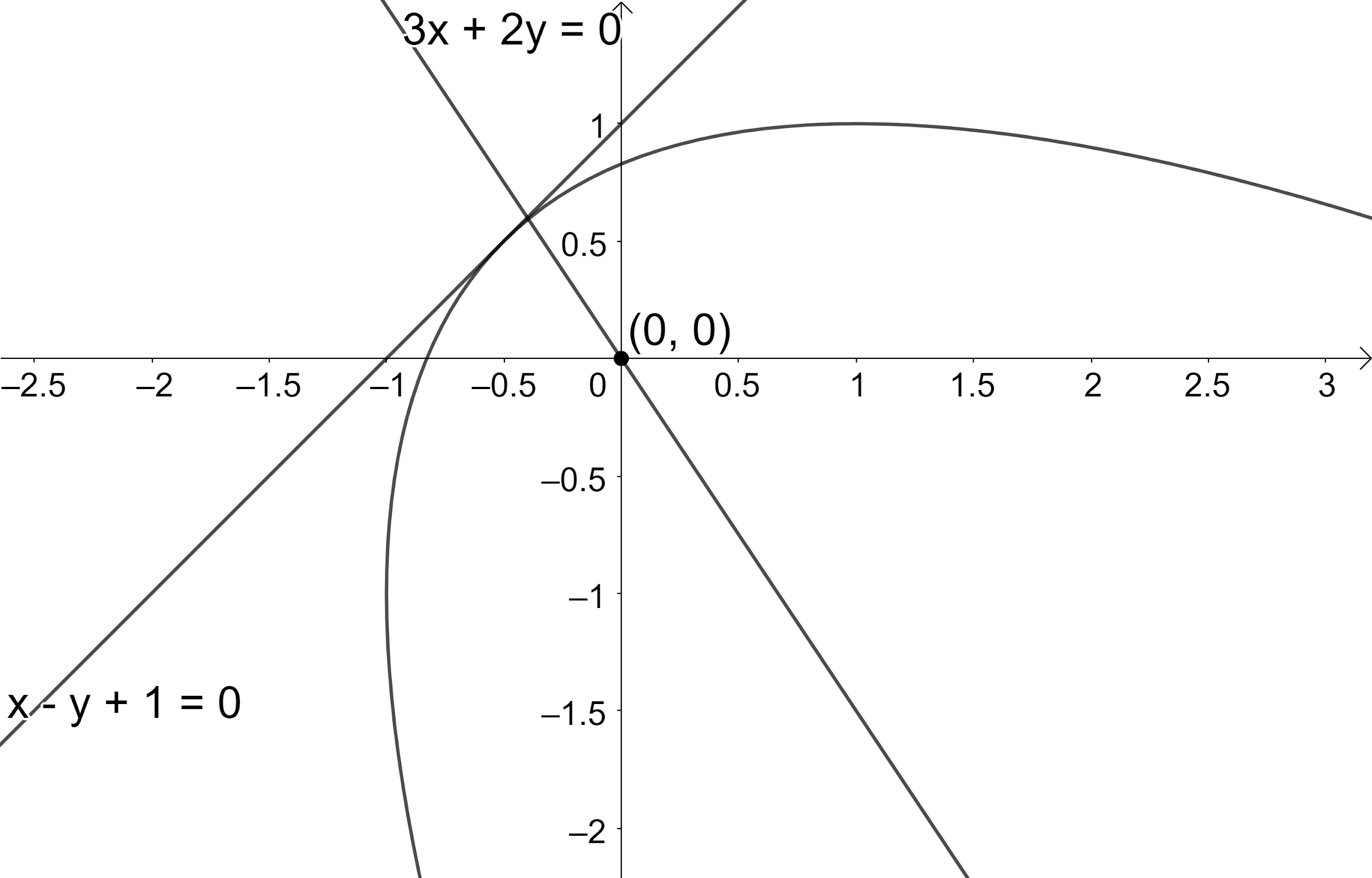
Let us substitute the point $\left( 0,0 \right)$ in the equation of line $3x+2y=0$.
So, we have $3\left( 0 \right)+2\left( 0 \right)=0$.
$\Rightarrow 0+0=0$.
$\Rightarrow 0=0$.
So, we have found that the chord $3x+2y=0$ passes through the focus of the parabola. We know that the chord of the parabola which passes through the focus in a parabola is known as focal chord.
So, we have found that $3x+2y=0$ is the focal chord of the given parabola.
We know that the tangents at the ends of the focal chord in a parabola intersects at right angles.
So, the tangents at the ends of the chord $3x+2y=0$ intersect at an angle $\dfrac{\pi }{2}$.

So, the correct answer is “Option c”.

Note: We can also solve this problem by rotating the equation of the axis at angle of $\dfrac{\pi }{4}$ anti-clockwise which gives us the equation of parabola that resembles the standard parabola. We should know that the focal chord of the parabola passes through the focus and will have both ends on the parabola. We can also solve this problem by finding the equation of directrix, parabola and then finding the slopes of tangents at the ends of parabola to get the required answer.