Question

Consider the hyperbola $H:{x^2} - {y^2} = 1$ and circle S with the center $N({x_2},0)$ . Suppose that H and S touch each other at a point $P({x_1},{y_1})$ with ${x_1} > 1$ and ${y_1} > 0$ . The common tangent to H and S at P intersects the x-axis at point M. if $(l,m)$ is the centroid of the triangle PMN, then the correct expression(s) is(are):
A. $\dfrac{{dl}}{{d{x_1}}} = 1 - \dfrac{1}{{3{x^2}}}$ for ${x_1} > 1$
B. $\dfrac{{dm}}{{d{x_1}}} = \dfrac{{{x_1}}}{{3\sqrt {{x_1}^2 - 1} }}$ for ${x_1} > 1$
C. $\dfrac{{dl}}{{d{x_1}}} = 1 + \dfrac{1}{{3{x^2}}}$ for ${x_1} > 1$
D. $\dfrac{{dm}}{{d{y_1}}} = \dfrac{1}{3}$ for ${y_1} > 0$

Answer 1

First we’ll write the equation of circle by assuming any value of radius. Now, we’ll equate the derivative at P for hyperbola and circle. Using that we’ll find the equation of the tangent at P, giving us the value of x-intercept. Now we’ve all the coordinates of the triangle, now using the centroid formula we’ll get the required answer.

Complete step-by-step answer:
Given data: $H:{x^2} - {y^2} = 1$
Circle S with the center $N({x_2},0)$ .
Let the radius of the circle be ‘r’
Therefore, the equation of the circle is ${\left( {x - {x_2}} \right)^2} + {y^2} = {r^2}$
Diagram:

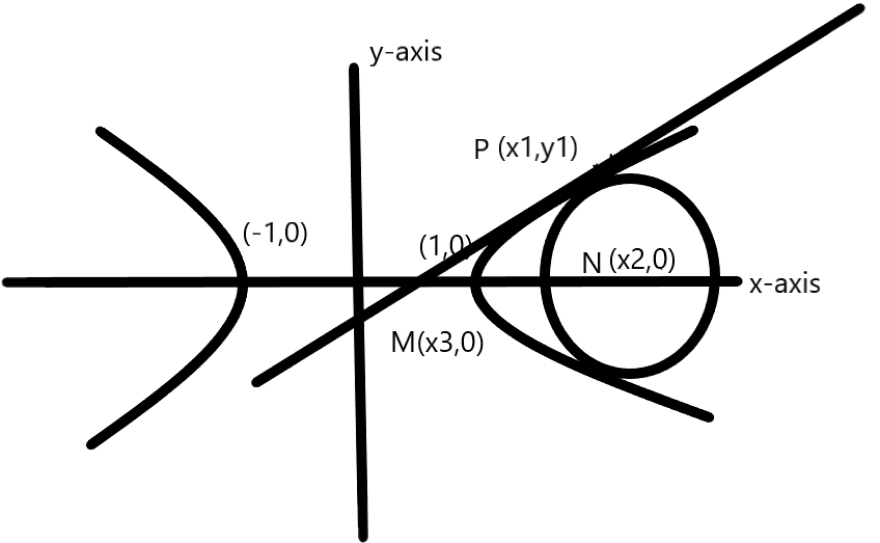
The equation of hyperbola is $H:{x^2} - {y^2} = 1$
On differentiating the equation of the hyperbola, we get,
$\Rightarrow 2x - 2y{\left( {\dfrac{{dy}}{{dx}}} \right)_H} = 0$
On simplification we get,
$\Rightarrow {\left( {\dfrac{{dy}}{{dx}}} \right)_H} = \dfrac{x}{y}$
The equation of the circle is ${\left( {x - {x_2}} \right)^2} + {y^2} = {r^2}$
Now, on differentiating the equation of circle
$\Rightarrow 2\left( {x - {x_2}} \right) + 2y{\left( {\dfrac{{dy}}{{dx}}} \right)_S} = 0$
On simplification we get,
$\Rightarrow {\left( {\dfrac{{dy}}{{dx}}} \right)_S} = \dfrac{{{x_2} - x}}{y}$
Since $P({x_1},{y_1})$ is the common point where the hyperbola and the circle touches each other,
So, the tangent will be equal at the point $P({x_1},{y_1})$
Hence at point $P({x_1},{y_1})$ , we have,
$\Rightarrow {\left( {\dfrac{{dy}}{{dx}}} \right)_S} = \dfrac{{{x_2} - {x_1}}}{{{y_1}}}$ and ${\left( {\dfrac{{dy}}{{dx}}} \right)_H} = \dfrac{{{x_1}}}{{{y_1}}}$
Also as the tangent will be equal so we have ${\left( {\dfrac{{dy}}{{dx}}} \right)_H} = {\left( {\dfrac{{dy}}{{dx}}} \right)_S}$ ,
Hence we get,
$\Rightarrow \dfrac{{{x_1}}}{{{y_1}}} = \dfrac{{{x_2} - {x_1}}}{{{y_1}}}$
Multiplying ${y_1}$ on both sides,
$\Rightarrow {x_1} = {x_2} - {x_1}$
On simplification we get,
$\Rightarrow 2{x_1} = {x_2}..............(i)$
Now, the equation of tangent will be as it passes through $P({x_1},{y_1})$
Hence the equation of tangent is,
$\Rightarrow (y - {y_1}) = \dfrac{{{x_1}}}{{{y_1}}}(x - {x_1})$
We know that for the x-intercept $y = 0$
$\Rightarrow - {y_1} = \dfrac{{{x_1}}}{{{y_1}}}(x - {x_1})$
On cross multiplication, we get,
$\Rightarrow - {y_1}^2 = {x_1}x - {x_1}^2$
On solving for x we get,
$\Rightarrow \dfrac{{{x_1}^2 - {y_1}^2}}{{{x_1}}} = x$
Therefore point M is $\left( {\dfrac{{{x_1}^2 - {y_1}^2}}{{{x_1}}},0} \right)$
Now we know that coordinate of the centroid of the triangle is given by the average of the points of its vertices
If all the three coordinate of triangle is known then centroid can be given as,
$c(\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3})$
So, now calculating as per the obtained coordinates as shown below,
$\Rightarrow (l,m) = \left( {\dfrac{{{x_1} + {x_2} + \dfrac{{{x_1}^2 - {y_1}^2}}{{{x_1}}}}}{3},\dfrac{{0 + {y_1} + 0}}{3}} \right)......................(ii)$
On comparing
$\Rightarrow l = \dfrac{{{x_1} + {x_2} + \dfrac{{{x_1}^2 - {y_1}^2}}{{{x_1}}}}}{3}$
Substituting the value of ${x_2}$ from equation(i)
$\Rightarrow l = \dfrac{{3{x_1} + \dfrac{{{x_1}^2 - {y_1}^2}}{{{x_1}}}}}{3}................(iii)$
We know that $P({x_1},{y_1})$ lie on hyperbola so it will satisfy the equation of the hyperbola
$\Rightarrow {x_1}^2 - {y_1}^2 = 1$
$\Rightarrow {x_1}^2 - 1 = {y_1}^2$
Substituting the value of ${y_1}^2$ in equation(iii)
$\Rightarrow l = \dfrac{{3{x_1} + \dfrac{{{x_1}^2 - {x_1}^2 + 1}}{{{x_1}}}}}{3}$
On simplification we get,
$\Rightarrow l = \dfrac{{3{x_1} + \dfrac{1}{{{x_1}}}}}{3}$
Now, on differentiating with-respect-to ${x_1}$ , we get,
$\Rightarrow \dfrac{{dl}}{{d{x_{}}}} = \dfrac{{3 - \dfrac{1}{{{x_1}^2}}}}{3}$
On simplification we get,
$\Rightarrow \dfrac{{dl}}{{d{x_1}}} = 1 - \dfrac{1}{{3{x_1}^2}}$
Now comparing the ordinate of equation(ii)
$\Rightarrow m = \dfrac{{0 + {y_1} + 0}}{3}$
On differentiating with-respect-to ${y_1}$
$\Rightarrow \dfrac{{dm}}{{d{y_1}}} = \dfrac{1}{3}$
Option(A) and (D) are correct.
Note: A hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows.
Write the equation of the tangent properly and differentiate the given equation in order to determine the slope of tangent
Also remember the concept of calculating centroid so that without any mistake, the required coordinates can be calculated.
A circle is a shape consisting of all points in a plane that are a given distance from a given point, the center; equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant.
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve.
In mathematics and physics, the centroid is the arithmetic mean position of all the points in the curve or any shape.