Question

Consider the hyperbola $9x^{2}-16y^{2}+72x-32y-16=0$. Find the following: (a) equation of auxilary circle (b) equation of director circle

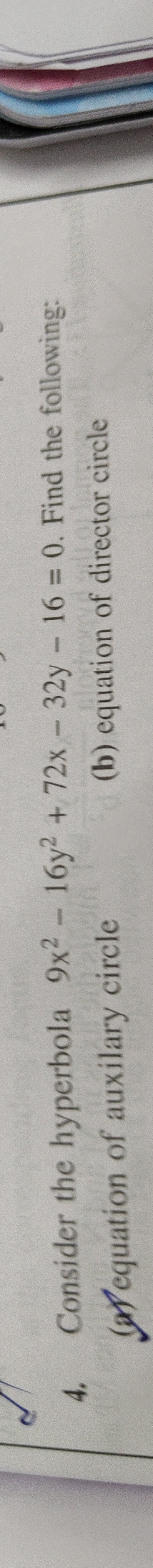
Answer 1

(a) $(x+4)^2 + (y+1)^2 = 16$ (b) $(x+4)^2 + (y+1)^2 = 7$

Answer 2

First, convert the hyperbola equation to standard form by completing the square: $9x^{2}-16y^{2}+72x-32y-16=0$ $9(x+4)^2 - 16(y+1)^2 = 144$ $\frac{(x+4)^2}{16} - \frac{(y+1)^2}{9} = 1$ The center is $(h,k) = (-4, -1)$, $a^2 = 16$, and $b^2 = 9$. (a) The auxiliary circle is $(x-h)^2 + (y-k)^2 = a^2$, which is $(x+4)^2 + (y+1)^2 = 16$. (b) The director circle is $(x-h)^2 + (y-k)^2 = a^2 - b^2$, which is $(x+4)^2 + (y+1)^2 = 16 - 9 = 7$.