Question

Consider the given trigonometric expression, ${{\cos }^{-1}}x=a+{{\tan }^{-1}}\dfrac{\sqrt{1-{{x}^{b}}}}{cx}$ for $x\le 0$. Find the value of $a,b$ and $c$.
(a) $a=\pi ,b=1,c=1$
(b) $a=-\pi ,b=2,c=2$
(c) $a=-\pi ,b=1,c=2$
(d) $a=\pi ,b=2,c=1$

Answer 1

Change ${{\cos }^{-1}}$ into ${{\tan }^{-1}}$ by assuming $x$ as base and 1 as perpendicular. Take both the ${{\tan }^{-1}}$ into left hand side and use the formula ${{\tan }^{-1}}x-{{\tan }^{-1}}y={{\tan }^{-1}}\left( \dfrac{x-y}{1+xy} \right)$ to convert it into single inverse function. Assume $a=\pm \pi$ according to the given options and accordingly compare L.H.S and R.H.S to determine the value of $a,b$ and $c$.

Complete step by step answer:
We have been given, ${{\cos }^{-1}}x=a+{{\tan }^{-1}}\dfrac{\sqrt{1-{{x}^{b}}}}{cx}$. We know that, $\cos \theta =\dfrac{\text{base}}{\text{Hypotenuse}}$. Therefore, ${{\cos }^{-1}}x$ will have the numerator ‘$x$’ as its base and the denominator ‘1’ as its hypotenuse.

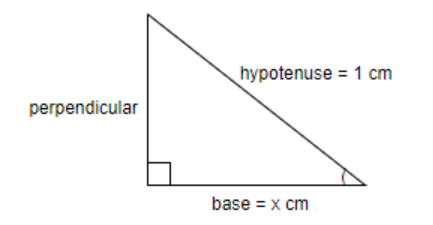
Therefore, using Pythagoras theorem: $\text {hypotenuse}^{2}=\text{perpendicular}^{2}+\text{base}^{2}$, we get,
$\begin{aligned} & \text{perpendicular}^{2}=\text {hypotenuse}^{2}-\text{base}^{2} \\\ & \Rightarrow \text{perpendicular}=\sqrt{\text {hypotenuse}^{2}-\text{base}^{2}} \\\ & \Rightarrow \text{perpendicular}=\sqrt{1-{{x}^{2}}} \\\ \end{aligned}$
$\therefore {{\cos }^{-1}}x={{\tan }^{-1}}\dfrac{\sqrt{1-{{x}^{2}}}}{x}$
Therefore, the equation becomes, ${{\tan }^{-1}}\dfrac{\sqrt{1-{{x}^{2}}}}{x}=a+{{\tan }^{-1}}\dfrac{\sqrt{1-{{x}^{b}}}}{cx}$. Now,
${{\tan }^{-1}}\dfrac{\sqrt{1-{{x}^{2}}}}{x}-{{\tan }^{-1}}\dfrac{\sqrt{1-{{x}^{b}}}}{cx}=a$
Applying the formula ${{\tan }^{-1}}x-{{\tan }^{-1}}y={{\tan }^{-1}}\left( \dfrac{x-y}{1+xy} \right)$ we get,
$\begin{aligned} & {{\tan }^{-1}}\left( \dfrac{\dfrac{\sqrt{1-{{x}^{2}}}}{x}-\dfrac{\sqrt{1-{{x}^{b}}}}{cx}}{1+\dfrac{\sqrt{1-{{x}^{2}}}}{x}\times \dfrac{\sqrt{1-{{x}^{b}}}}{cx}} \right)=a \\\ & \Rightarrow \left( \dfrac{\dfrac{\sqrt{1-{{x}^{2}}}}{x}-\dfrac{\sqrt{1-{{x}^{b}}}}{cx}}{1+\dfrac{\sqrt{1-{{x}^{2}}}}{x}\times \dfrac{\sqrt{1-{{x}^{b}}}}{cx}} \right)=\tan a \\\ \end{aligned}$
Now, when we see the given options carefully, we observe that $a$ is either, $\pi \text{ or }-\pi$. We know that, $\tan \pi =\tan (-\pi )=0$. Therefore, $\tan a$ must be zero.
$\begin{aligned} & \Rightarrow \left( \dfrac{\dfrac{\sqrt{1-{{x}^{2}}}}{x}-\dfrac{\sqrt{1-{{x}^{b}}}}{cx}}{1+\dfrac{\sqrt{1-{{x}^{2}}}}{x}\times \dfrac{\sqrt{1-{{x}^{b}}}}{cx}} \right)=0 \\\ & \Rightarrow \dfrac{\sqrt{1-{{x}^{2}}}}{x}-\dfrac{\sqrt{1-{{x}^{b}}}}{cx}=0 \\\ & \Rightarrow \dfrac{\sqrt{1-{{x}^{2}}}}{x}=\dfrac{\sqrt{1-{{x}^{b}}}}{cx} \\\ \end{aligned}$
Now, on comparing the left hand side and right hand side, we get,
‘$b$’ must be 2 and ‘$c$’ must be 1.

So, the correct answer is “Option d”.

Note: In the above solution we have changed ${{\cos }^{-1}}$ into ${{\tan }^{-1}}$. We can also apply the reverse process, that is, to change ${{\tan }^{-1}}$ into ${{\cos }^{-1}}$. But, the next problem that we will encounter is that we will get an equation that will be pretty difficult to solve. Therefore, it is always convenient to convert the different inverse functions into ${{\tan }^{-1}}$.