Question
Question: Consider the given population-year graph with population along the y-axis and the years along the x-...
Consider the given population-year graph with population along the y-axis and the years along the x-axis(Graph not to scale).
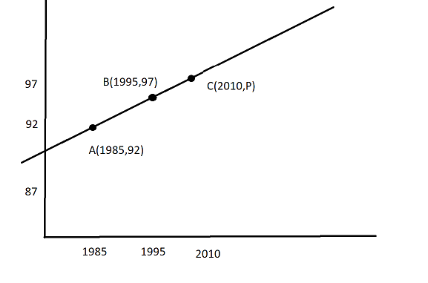
Find the slope of the line AB and use that to find what will be the population in 2010.
Solution
Hint: Use the fact that the slope of the line joining the points A(x1,y1) and B(x2,y2) is given by
m=x2−x1y2−y1.
Hence find the slope of the line AB.
Complete step-by-step answer:
Again using the above formula find the slope of the line BC in terms of P. Since AB and BC are the same lines, the slopes are equal. Equate the two slopes and hence form an equation in P. Solve for P. The value of P gives the population in the year 2010.

Finding the slope of AB:
We have A≡(1985,92) and B≡(1995,97)
We know that the slope of the line joining the points A(x1,y1) and B(x2,y2) is given by
m=x2−x1y2−y1.
Here x1=1985,x2=1995,y1=92 and y2=97
Hence the slope of AB is given by m=1995−198597−92=105=21
Finding the slope of the line BC:
We have B≡(1995,97) and C≡(2010,P)
We know that the slope of the line joining the points A(x1,y1) and B(x2,y2) is given by
m=x2−x1y2−y1.
Here x1=1995,x2=2010,y1=97 and y2=P
Hence the slope of BC is given by m=2010−1995P−97=15P−97
Since AB and BC are the same lines, we have
15P−97=21
Cross multiplying, we get
2P−194=15
Adding 194 on both sides, we get
2P=209
Dividing by 2 on both sides, we get
P=2209=104.5
Hence the population in 2010 is 104.5 units.
Note: Alternative solution:
Let the equation of AB be y = mx+c
Since the point (1985,92) lies on the line, we have
1985m+c=92
Since the point (1995,97) lies on the line, we have
1995m+c=97
Hence, we have
1995m−1985m=97−92⇒10m=5⇒m=21
Hence, we have
c=92−21985=92−992.5=−900.5
Since (2010,P) lies on the line, we have
P=21(2010)−900.5=1005−900.5=104.5
Hence the slope of the line is 21 and the population in the year 2010 will be 104.5 units.
