Question

Consider the functions $f(x) = \left| {x - 2} \right| + \left| {x - 5} \right|,x \in R$
Statement 1 : $f'(4) = 0$
Statement 2 : $f$is continuous in $\left[ {2,5} \right],$ differentiable in $\left( {2,5} \right)$ and $f(2) = f(5)$
A). Statement 1 is false, statement 2 is true.
B). Statement 1 is true, statement 2 is true; statement 2 is the correct explanation for statement 1.
C). Statement 1 is true, statement 2 is true; statement 2 is incorrect explanation for statement 1.
D). Statement 1 is true, statement 2 is false.

Answer 1

This is a very simple problem though it may seem to be complex. Here given the function involved with two parts involved with modulus. This function is subdivided according to different intervals with respect to x. In order to solve this we should do it according to the differentiability and continuity of the given function.

Complete step-by-step solution:
First subdividing the intervals with respect to $x$ and due to the presence of the modulus.
First considering the first part of the function $f(x)$ which is $\left| {x - 2} \right|$
\Rightarrow \left| {x - 2} \right| = \left\\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {(x - 2)}&{\begin{array}{*{20}{c}} ;&{x > 2} \end{array}} \end{array}} \\\ {\begin{array}{*{20}{c}} { - (x - 2)}&{\begin{array}{*{20}{c}} ;&{x < 2} \end{array}} \end{array}} \end{array}} \right.
\Rightarrow \left| {x - 2} \right| = \left\\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {x - 2}&{\begin{array}{*{20}{c}} ;&{x > 2} \end{array}} \end{array}} \\\ {2\begin{array}{*{20}{c}} { - x}&{\begin{array}{*{20}{c}} ;&{x < 2} \end{array}} \end{array}} \end{array}} \right.
Now considering the second part of the function $f(x)$ which is $\left| {x - 5} \right|$
\Rightarrow \left| {x - 5} \right| = \left\\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {(x - 5)}&{\begin{array}{*{20}{c}} ;&{x > 5} \end{array}} \end{array}} \\\ {\begin{array}{*{20}{c}} { - (x - 5)}&{\begin{array}{*{20}{c}} ;&{x < 5} \end{array}} \end{array}} \end{array}} \right.
\Rightarrow \left| {x - 5} \right| = \left\\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {x - 5}&{\begin{array}{*{20}{c}} ;&{x > 5} \end{array}} \end{array}} \\\ {5\begin{array}{*{20}{c}} { - x}&{\begin{array}{*{20}{c}} ;&{x < 5} \end{array}} \end{array}} \end{array}} \right.
The first part of the function $f(x)$ which is $\left| {x - 2} \right|$ can be also written as, given below:
\Rightarrow \left| {x - 2} \right| = \left\\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {2 - x} \\\ {x - 2} \end{array}}&{\begin{array}{*{20}{c}} ; \\\ ; \end{array}}&{\begin{array}{*{20}{c}} {x < 2} \\\ {2 \leqslant x \leqslant 5} \end{array}} \end{array}} \right.
Now the second part of the function $f(x)$ which is $\left| {x - 5} \right|$ can be also written as, given below:
\Rightarrow \left| {x - 5} \right| = \left\\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {5 - x} \\\ {x - 5} \end{array}}&{\begin{array}{*{20}{c}} ; \\\ ; \end{array}}&{\begin{array}{*{20}{c}} {2 \leqslant x \leqslant 5} \\\ {x > 5} \end{array}} \end{array}} \right.
Now the whole function $f(x) = \left| {x - 2} \right| + \left| {x - 5} \right|$ is divided, as given below:
\Rightarrow \left| {x - 2} \right| + \left| {x - 5} \right| = \left\\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\left( {2 - x} \right) + \left( {5 - x} \right)} \\\ {\left( {x - 2} \right) + \left( {5 - x} \right)} \\\ {\left( {x - 2} \right) + \left( {x - 5} \right)} \end{array}}&{\begin{array}{*{20}{c}} ; \\\ ; \\\ ; \end{array}}&{\begin{array}{*{20}{c}} {x < 2} \\\ {2 \leqslant x \leqslant 5} \\\ {x > 5} \end{array}} \end{array}} \right.
\Rightarrow f(x) = \left| {x - 2} \right| + \left| {x - 5} \right| = \left\\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {7 - 2x} \\\ 3 \\\ {2x - 7} \end{array}}&{\begin{array}{*{20}{c}} ; \\\ ; \\\ ; \end{array}}&{\begin{array}{*{20}{c}} {x < 2} \\\ {2 \leqslant x \leqslant 5} \\\ {x > 5} \end{array}} \end{array}} \right.
Plotting the graph of the obtained function $f(x) = \left| {x - 2} \right| + \left| {x - 5} \right|$, as given below:

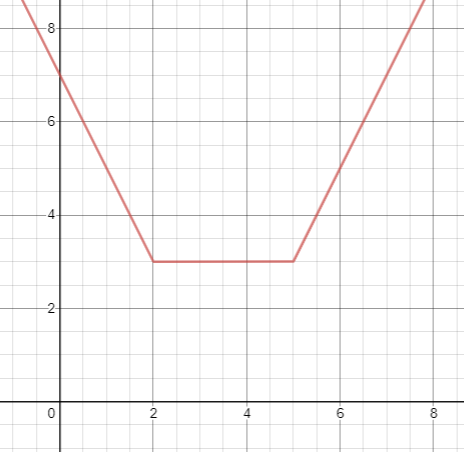
The graph decreases according to the equation $7 - 2x$ for the values of $x < 2$.
The graph remains constant according to the equation $y = 3$ for the values of $2 \leqslant x \leqslant 5$.
The graph increases according to the equation $2x - 7$ for the values of $x > 2$.
Now checking the statement 1, if it is correct, it is given that $f'(4) = 0$,
Here the graph remains constant for the values of $x$ from 2 to 5.
$\Rightarrow f(4) = 3$
$\Rightarrow f'(4) = 0$
Hence the statement 1 is correct.
Now checking the statement 2, if$f$is continuous in $\left[ {2,5} \right],$ differentiable in $\left( {2,5} \right)$ and $f(2) = f(5)$, as given below:
Here the graph remains constant for the values of $x$ from 2 to 5.
Checking the continuity for $x = 3,$ as given below:
$\Rightarrow \mathop {\lim }\limits_{x \to {3^ - }} f(x) = 3$
$\Rightarrow \mathop {\lim }\limits_{x \to {3^ + }} f(x) = 3$
Hence the function is both left and right continuous and differentiable.
$\Rightarrow f(2) = 3$
$\Rightarrow f(5) = 3$
$\therefore f(2) = f(5)$
Also the function$f$is continuous in $\left[ {2,5} \right],$ differentiable in $\left( {2,5} \right)$ and $f(2) = f(5)$.
Hence statement 2 is also true.
Statement 1 and 2 both are true.
But statement 2 is not the correct explanation for statement 1.
Statement 1 is true, statement 2 is true; statement 2 is incorrect explanation for statement 1.

Note: While solving this problem we should understand that the distributed function according to intervals the function is constant during the interval of x when x is less than 2 and greater than 2. The function is actually parallel to the horizontal axis, and hence the slope of the function during this interval will be obviously equal to zero, as the differentiation of a constant is zero.