Question

Consider the function $f(x)=x^2+x^2\int_{-1}^{1}tf(t)dt+x^3\int_{-1}^{1}f(t)dt$. The reciprocal of maximum value of $f(-x), x>0$ is equal to

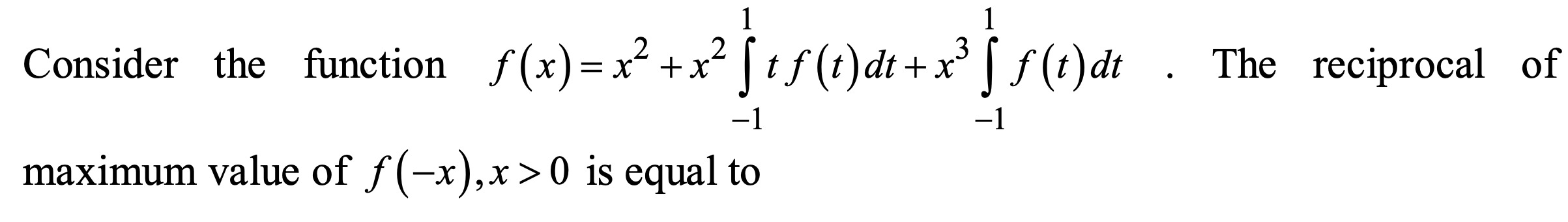
Answer 1

\frac{11}{5}

Answer 2

Let

$$A=\int_{-1}^{1} t\,f(t)\,dt,\quad B=\int_{-1}^{1} f(t)\,dt.$$

Then

$$f(x) = x^2 + x^2 A + x^3 B = (1+A)x^2 + Bx^3.$$

1. Compute A:

$$A=\int_{-1}^{1} t\Big[(1+A)t^2+Bt^3\Big]dt=(1+A)\int_{-1}^{1}t^3dt+B\int_{-1}^{1}t^4dt.$$

Since $\int_{-1}^{1}t^3dt=0$ (odd function) and $\int_{-1}^{1}t^4dt=\frac{2}{5}$,

$$A=\frac{2}{5}B.$$

2. Compute B:

$$B=\int_{-1}^{1}\Big[(1+A)t^2+Bt^3\Big]dt=(1+A)\int_{-1}^{1}t^2dt.$$

With $\int_{-1}^{1}t^2dt=\frac{2}{3}$,

$$B=\frac{2}{3}(1+A).$$

Substitute $A=\frac{2}{5}B$ into the equation:

$$B=\frac{2}{3}\left(1+\frac{2}{5}B\right)=\frac{2}{3}+\frac{4}{15}B.$$

Solve for $B$:

$$B-\frac{4}{15}B=\frac{2}{3}\quad\Longrightarrow\quad \frac{11}{15}B=\frac{2}{3}\quad\Longrightarrow\quad B=\frac{2}{3}\times\frac{15}{11}=\frac{10}{11}.$$

Then,

$$A=\frac{2}{5}\times \frac{10}{11}=\frac{4}{11}.$$

Thus,

$$f(x)=\left(1+\frac{4}{11}\right)x^2+\frac{10}{11}x^3=\frac{15}{11}x^2+\frac{10}{11}x^3.$$

3. Determine maximum of $f(-x)$ for $x>0$:

$$f(-x)=\frac{15}{11}x^2-\frac{10}{11}x^3=\frac{1}{11}\big[15x^2-10x^3\big].$$

Let $g(x)=15x^2-10x^3$. Differentiating,

$$g'(x)=30x-30x^2=30x(1-x).$$

Set $g'(x)=0$ $\Rightarrow x=0$ or $x=1$. For $x>0$, maximum at $x=1$. Thus,

$$\max(f(-x))=f(-1)=\frac{1}{11}\big[15(1)^2-10(1)^3\big]=\frac{5}{11}.$$

The reciprocal of the maximum is

$$\frac{11}{5}.$$