Question

Consider the function f(x) = x² + bx + c, where D=b²-4c > 0

Column I	Column II
Condition on b and	Number of point of non-differentiability of g(x) =
a b<0, c > 0	p 1
b c=0, b<0	q 2
c c=0, b>0	r 3
d b=0, c<0	s 5

Answer 1

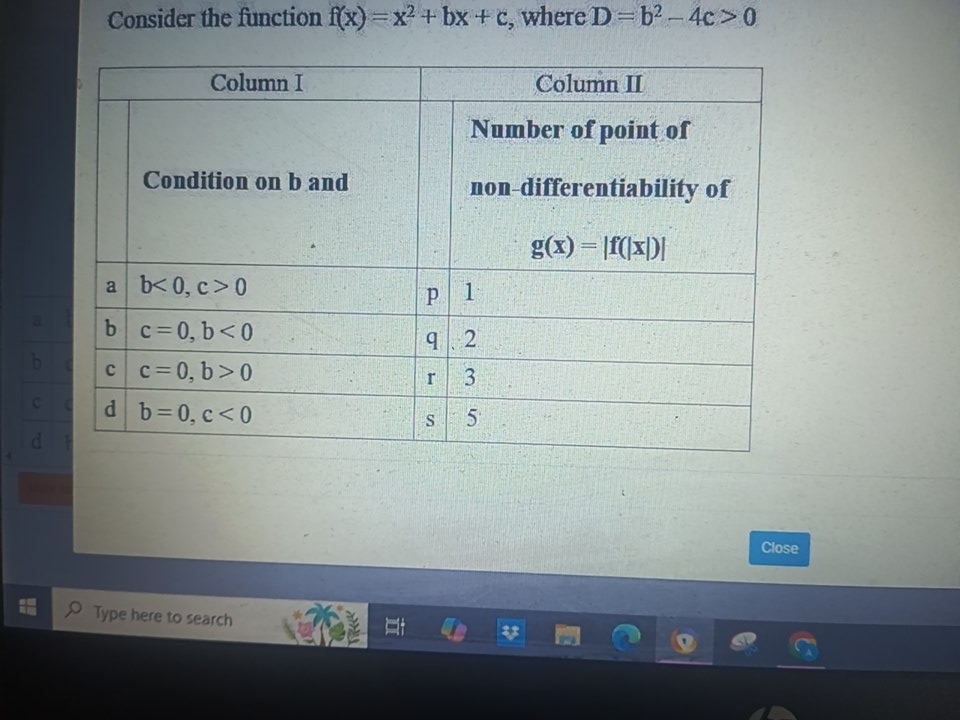
a-s, b-r, c-p, d-q

Answer 2

To determine the number of points of non-differentiability of $g(x) = |f(|x|)|$, where $f(x) = x^2 + bx + c$ and $D=b^2-4c > 0$, we analyze the function step-by-step.

Let $h(x) = f(|x|)$. Then $g(x) = |h(x)|$. The function $g(x) = |h(x)|$ is non-differentiable at points where:

1. $h(x)$ is non-differentiable.
2. $h(x)=0$ and $h'(x) \ne 0$ (i.e., the graph of $h(x)$ crosses the x-axis at a non-zero slope).

Let's analyze $h(x) = f(|x|)$: $h(x) = \begin{cases} f(x) = x^2 + bx + c & \text{if } x \ge 0 \\ f(-x) = (-x)^2 + b(-x) + c = x^2 - bx + c & \text{if } x < 0 \end{cases}$

Differentiability of $h(x)$ at $x=0$: $h'(x) = \begin{cases} 2x + b & \text{if } x > 0 \\ 2x - b & \text{if } x < 0 \end{cases}$ Right-hand derivative: $h'(0^+) = b$ Left-hand derivative: $h'(0^-) = -b$ For $h(x)$ to be differentiable at $x=0$, we need $b = -b \implies 2b=0 \implies b=0$. So, if $b \ne 0$, $h(x)$ is non-differentiable at $x=0$.

Now we analyze each case:

Case (a): b < 0, c > 0

1. Differentiability of $h(x)$ at $x=0$: Since $b<0$, $b \ne 0$. So $h(x)$ is non-differentiable at $x=0$. At $x=0$, $h(0) = f(0) = c$. Since $c>0$, $h(0) \ne 0$. If $h(x)$ is non-differentiable at $x=0$ and $h(0) \ne 0$, then $g(x)=|h(x)|$ is also non-differentiable at $x=0$. (1 point)

2. Roots of $h(x)=0$: $h(x) = f(|x|) = 0$. The roots of $f(x)=x^2+bx+c=0$ are $r_1, r_2 = \frac{-b \pm \sqrt{D}}{2}$. Since $c = r_1 r_2 > 0$, the roots have the same sign. Since $-b = r_1+r_2 > 0$ (because $b<0$), the roots are both positive. Let $0 < r_1 < r_2$. So, $f(|x|)=0$ implies $|x|=r_1$ or $|x|=r_2$. This gives $x = \pm r_1$ and $x = \pm r_2$. These are 4 distinct non-zero roots: $-r_2, -r_1, r_1, r_2$. Let's check $h'(x)$ at these roots: For $x>0$: $h'(x) = f'(x) = 2x+b$. $h'(r_1) = 2r_1+b = \pm \sqrt{D} \ne 0$. $h'(r_2) = 2r_2+b = \mp \sqrt{D} \ne 0$. For $x<0$: $h'(x) = 2x-b$. $h'(-r_1) = 2(-r_1)-b = -2r_1-b = -(2r_1+b) \ne 0$. $h'(-r_2) = 2(-r_2)-b = -2r_2-b = -(2r_2+b) \ne 0$. Since $h(x)=0$ and $h'(x) \ne 0$ at these 4 roots, $g(x)=|h(x)|$ is non-differentiable at these 4 points. (4 points) Total non-differentiability points = $1+4=5$. Matches (s).

Case (b): c = 0, b < 0

1. Differentiability of $h(x)$ at $x=0$: Since $b<0$, $b \ne 0$. So $h(x)$ is non-differentiable at $x=0$. At $x=0$, $h(0) = f(0) = c = 0$. Since $h(0)=0$ and $h'(0^+) = b \ne 0$ and $h'(0^-) = -b \ne 0$, $g(x)=|h(x)|$ is non-differentiable at $x=0$. (1 point)

2. Roots of $h(x)=0$: $f(x)=x^2+bx = x(x+b)$. Roots are $0, -b$. Since $b<0$, $-b > 0$. Let $a=-b$. So roots are $0, a$ where $a>0$. $f(|x|)=0$ implies $|x|=0$ or $|x|=a$. This gives $x=0, x=\pm a$. These are 3 distinct roots: $-a, 0, a$. We already accounted for $x=0$. Let's check $h'(x)$ at $x=a$ (positive root) and $x=-a$ (negative root): For $x>0$: $h'(x) = 2x+b$. $h'(a) = 2a+b = 2(-b)+b = -b$. Since $b \ne 0$, $-b \ne 0$. So $x=a$ is a non-differentiable point. For $x<0$: $h'(x) = 2x-b$. $h'(-a) = 2(-a)-b = -2a-b = -2(-b)-b = 2b-b = b$. Since $b \ne 0$, $b \ne 0$. So $x=-a$ is a non-differentiable point. (2 points from $\pm a$) Total non-differentiability points = $1+2=3$. Matches (r).

Case (c): c = 0, b > 0

1. Differentiability of $h(x)$ at $x=0$: Since $b>0$, $b \ne 0$. So $h(x)$ is non-differentiable at $x=0$. At $x=0$, $h(0) = f(0) = c = 0$. Since $h(0)=0$ and $h'(0^+) = b \ne 0$ and $h'(0^-) = -b \ne 0$, $g(x)=|h(x)|$ is non-differentiable at $x=0$. (1 point)

2. Roots of $h(x)=0$: $f(x)=x^2+bx = x(x+b)$. Roots are $0, -b$. Since $b>0$, $-b < 0$. $f(|x|)=0$ implies $|x|=0$ or $|x|=-b$. Since $-b<0$, $|x|=-b$ has no real solutions. So the only root of $h(x)=0$ is $x=0$. We have already accounted for $x=0$. No other roots. Total non-differentiability points = $1$. Matches (p).

Case (d): b = 0, c < 0

1. Differentiability of $h(x)$ at $x=0$: Since $b=0$, $h'(0^+) = 0$ and $h'(0^-) = 0$. So $h(x)$ is differentiable at $x=0$. Also, $h(x) = f(|x|) = x^2+c$ for $x \ge 0$ and $h(x) = f(-x) = x^2+c$ for $x < 0$. So $h(x) = x^2+c$ for all $x \in \mathbb{R}$. Thus, $g(x) = |x^2+c|$.

2. Roots of $g(x)=0$: $g(x)=0 \implies x^2+c=0$. Since $D=b^2-4c > 0$ and $b=0$, we have $-4c > 0 \implies c < 0$. Let $c=-a^2$ for some $a>0$. Then $x^2-a^2=0 \implies (x-a)(x+a)=0 \implies x=\pm a$. These are 2 distinct non-zero roots: $-a, a$. Let $u(x) = x^2+c$. Then $g(x)=|u(x)|$. $u'(x) = 2x$. At $x=a$: $u(a)=0$. $u'(a)=2a$. Since $a>0$, $u'(a) \ne 0$. So $x=a$ is a non-differentiable point. At $x=-a$: $u(-a)=0$. $u'(-a)=-2a$. Since $a>0$, $u'(-a) \ne 0$. So $x=-a$ is a non-differentiable point. Total non-differentiability points = $2$. Matches (q).

Final mapping: a $\to$ s (5 points) b $\to$ r (3 points) c $\to$ p (1 point) d $\to$ q (2 points)

The final answer is $\boxed{a-s, b-r, c-p, d-q}$.

The question is a matching type question, and the solution provides the matches.