Question

Consider the function

$f(x) = \begin{cases} x + x^2 \cos(\frac{\pi}{x}), x \neq 0 \\ 0 , x = 0 \end{cases}$

consider the following statements. Then which of the following is/are correct?

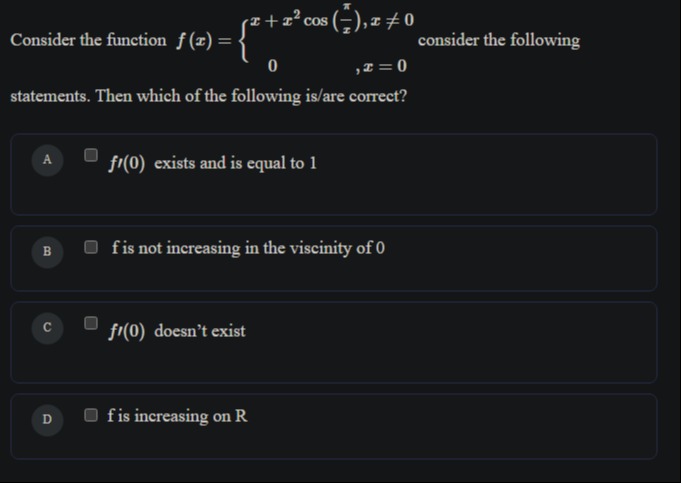
• A. $f'(0)$ exists and is equal to 1
• B. f is not increasing in the viscinity of 0
• C. $f'(0)$ doesn't exist
• D. f is increasing on R

Answer 1

Answer: (A), (B)

A, B

Answer 2

To analyze the given function $f(x)$ and the statements, we will evaluate the derivative at $x=0$ and examine the behavior of $f'(x)$ in the vicinity of $x=0$.

The function is defined as: $f(x) = \begin{cases} x + x^2 \cos(\frac{\pi}{x}), & x \neq 0 \\ 0, & x = 0 \end{cases}$

Part 1: Evaluate $f'(0)$

We use the definition of the derivative at a point: $f'(0) = \lim_{h \to 0} \frac{f(0+h) - f(0)}{h}$

Substitute the function definition: $f'(0) = \lim_{h \to 0} \frac{(h + h^2 \cos(\frac{\pi}{h})) - 0}{h}$ $f'(0) = \lim_{h \to 0} \frac{h(1 + h \cos(\frac{\pi}{h}))}{h}$

For $h \neq 0$, we can cancel $h$: $f'(0) = \lim_{h \to 0} (1 + h \cos(\frac{\pi}{h}))$

We know that $-1 \le \cos(\frac{\pi}{h}) \le 1$. Multiplying by $h$ (assuming $h>0$, if $h<0$ then the inequalities reverse but the absolute value bound remains): $-|h| \le h \cos(\frac{\pi}{h}) \le |h|$

As $h \to 0$, by the Squeeze Theorem, $h \cos(\frac{\pi}{h}) \to 0$. Therefore, $f'(0) = 1 + 0 = 1$.

Statement A: $f'(0)$ exists and is equal to 1.

Based on our calculation, this statement is correct.

Statement C: $f'(0)$ doesn't exist.

Since we found $f'(0) = 1$, this statement is incorrect.

Part 2: Analyze the increasing/decreasing nature of $f(x)$ in the vicinity of 0

For $f(x)$ to be increasing in the vicinity of 0, there must exist an open interval $(-\delta, \delta)$ for some $\delta > 0$ such that $f(x)$ is increasing on this interval. For a differentiable function, this implies that $f'(x) \ge 0$ for all $x \in (-\delta, \delta)$.

First, let's find $f'(x)$ for $x \neq 0$: $f'(x) = \frac{d}{dx} (x + x^2 \cos(\frac{\pi}{x}))$

Using the product rule and chain rule: $f'(x) = 1 + (2x \cos(\frac{\pi}{x}) + x^2 (-\sin(\frac{\pi}{x})) (-\frac{\pi}{x^2}))$ $f'(x) = 1 + 2x \cos(\frac{\pi}{x}) + \pi \sin(\frac{\pi}{x})$

Now, let's check the sign of $f'(x)$ as $x \to 0$. The term $2x \cos(\frac{\pi}{x})$ approaches 0 as $x \to 0$ (by Squeeze Theorem, similar to $h \cos(\frac{\pi}{h})$). However, the term $\pi \sin(\frac{\pi}{x})$ oscillates between $-\pi$ and $\pi$ as $x \to 0$.

Consider a sequence of points $x_k$ approaching 0 from the positive side, such that $\sin(\frac{\pi}{x_k})$ takes a specific value. Let $\frac{\pi}{x_k} = \frac{3\pi}{2} + 2k\pi$ for large positive integer $k$. This implies $\frac{1}{x_k} = \frac{3}{2} + 2k = \frac{3+4k}{2}$, so $x_k = \frac{2}{3+4k}$. As $k \to \infty$, $x_k \to 0^+$. At these points, $\sin(\frac{\pi}{x_k}) = \sin(\frac{3\pi}{2} + 2k\pi) = \sin(\frac{3\pi}{2}) = -1$. And $\cos(\frac{\pi}{x_k}) = \cos(\frac{3\pi}{2} + 2k\pi) = \cos(\frac{3\pi}{2}) = 0$.

Substitute these into $f'(x)$: $f'(x_k) = 1 + 2x_k \cos(\frac{\pi}{x_k}) + \pi \sin(\frac{\pi}{x_k})$ $f'(x_k) = 1 + 2(\frac{2}{3+4k})(0) + \pi(-1)$ $f'(x_k) = 1 - \pi$

Since $\pi \approx 3.14159$, $1 - \pi \approx 1 - 3.14159 = -2.14159$, which is a negative value. This means that for any arbitrarily small positive $\delta$, we can find a point $x_k = \frac{2}{3+4k}$ (by choosing $k$ large enough such that $x_k < \delta$) in the interval $(0, \delta)$ where $f'(x_k) < 0$. Since $f'(x)$ takes negative values in any neighborhood of 0, the function $f(x)$ cannot be increasing in the vicinity of 0.

Statement B: f is not increasing in the vicinity of 0.

Based on our analysis, this statement is correct.

Statement D: f is increasing on R.

Since $f(x)$ is not increasing in the vicinity of 0, it cannot be increasing on the entire real line R. This statement is incorrect.

Conclusion:

Statements A and B are correct.

The final answer is $\boxed{A, B}$

Explanation of the solution:

1. Calculate $f'(0)$: Use the definition of the derivative $f'(0) = \lim_{h \to 0} \frac{f(h) - f(0)}{h}$. Substitute $f(h) = h + h^2 \cos(\frac{\pi}{h})$ and $f(0)=0$. This simplifies to $\lim_{h \to 0} (1 + h \cos(\frac{\pi}{h}))$. By the Squeeze Theorem, $h \cos(\frac{\pi}{h}) \to 0$ as $h \to 0$. Thus, $f'(0) = 1$. This confirms statement A and refutes statement C.
2. Determine if $f$ is increasing near 0: Calculate $f'(x)$ for $x \neq 0$: $f'(x) = 1 + 2x \cos(\frac{\pi}{x}) + \pi \sin(\frac{\pi}{x})$. For $f$ to be increasing in the vicinity of 0, $f'(x)$ must be non-negative in some interval around 0. Consider points $x_k = \frac{2}{3+4k}$ as $k \to \infty$. These points approach 0. At these points, $\sin(\frac{\pi}{x_k}) = -1$ and $\cos(\frac{\pi}{x_k}) = 0$. Substituting these into $f'(x)$, we get $f'(x_k) = 1 - \pi$. Since $1 - \pi < 0$, $f'(x)$ takes negative values arbitrarily close to 0. Therefore, $f(x)$ is not increasing in the vicinity of 0. This confirms statement B and refutes statement D.