Solveeit Logo
Login

Question

Question: Consider the function, \(f\left( x \right)={{\cos }^{-1}}x-{{\sin }^{-1}}x.\) On the basis of above ...

Consider the function, f(x)=cos⁡−1x−sin⁡−1x.f\left( x \right)={{\cos }^{-1}}x-{{\sin }^{-1}}x. On the basis of above information answer the given question.
Number of solutions of the equation f(x)=tan⁡−1xf\left( x \right)={{\tan }^{-1}}x is,
A.3
B.2
C.1
D.0

Explanation

Solution

To solve this question, we need to know the various relations between the different inverse trigonometric functions. We also need to know how to plot these inverse trigonometric functions on the graph. We plot the two curves one for f(x)=cos⁡−1x−sin⁡−1xf\left( x \right)={{\cos }^{-1}}x-{{\sin }^{-1}}x and the other for f(x)=tan⁡−1xf\left( x \right)={{\tan }^{-1}}x . We then locate the intersection points and the number of intersection points give us the number of solutions for the given equation.

Complete step by step solution:
In order to solve such questions, it is very important to know the concept of inverse trigonometric functions and their basic curves in order to plot them. The function given in the questions is,
⇒f(x)=cos⁡−1x−sin⁡−1x\Rightarrow f\left( x \right)={{\cos }^{-1}}x-{{\sin }^{-1}}x
We first plot this function in the graph by substituting various values for x and obtain the values of the function at that point.
The plot for this curve is represented by the green curve in the figure below.

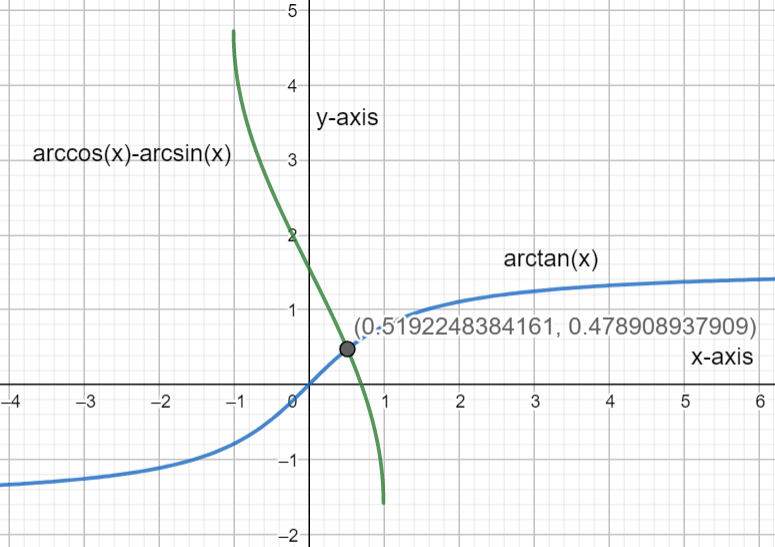
Now we need to plot the graph for the equation when f(x)=tan⁡−1xf\left( x \right)={{\tan }^{-1}}x . This is plotted in the same manner as the first curve and we obtain the curve represented by the blue curve in the figure. Another way to represent this inverse function is by the use of arccos⁡(x)\arccos \left( x \right) which is same as cos⁡−1x.{{\cos }^{-1}}x.
We now need to locate the number of points at which the two curves intersect. There exists only one intersection point for these two curves which represents that for the equation given in question, which is cos⁡−1x−sin⁡−1x=tan⁡−1x{{\cos }^{-1}}x-{{\sin }^{-1}}x={{\tan }^{-1}}x has only 1 value of x as its solution. This solution exists at the point (0.5192,0.4789).\left( 0.5192,0.4789 \right).
Hence, the number of solutions for the given question is 1. Hence, the correct option is C.

Note: It is essential to know the basic trigonometric inverses and the various relations between them. We can also solve this question by making use of the standard relations between the inverse trigonometric functions to solve the equation given in question which is cos⁡−1x−sin⁡−1x=tan⁡−1x.{{\cos }^{-1}}x-{{\sin }^{-1}}x={{\tan }^{-1}}x. One important tip here is that there are two ways to represent inverse trigonometric functions: one is cos⁡−1x{{\cos }^{-1}}x and another one is arccos⁡(x).\arccos \left( x \right). Both can be used interchangeably and they mean the same.