Question

Consider the following venn diagram:

(A) Shade the following sets:
(i) $C' \cap \left( {A \cup B} \right)$
(ii) $\left( {A \cap B} \right) \cup \left( {B \cap C} \right)$
(B) Given $n(A) = 10,n(B) = 7,n({\text{only }}C) = 15$. Find the value of:
(i) $n\left( {A \cap B} \right)$
(ii) $n\left( {A \cup B} \right)$

Answer 1

In this question, we are given a venn diagram and we have been asked to shade the region made by the given sets in part (a). Start by shading the question in parts and see the common part between the two parts. That part will be your answer.
In part (B), we have been asked the value of certain sets. You can either solve by using formulas or just by looking at the diagram.

Complete step-by-step answer:
We are given a venn diagram. Let us solve the question step by step.
(A) (i) We have to shade the region represented by $C' \cap \left( {A \cup B} \right)$. First, we will shade the region represented by $C'$, and the region represented by $(A \cup B)$.

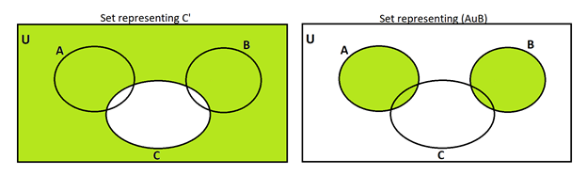
$C' = U - C$
Now, since we have been asked the common part between them, notice the common area.
The common area between the two figures is shown below:

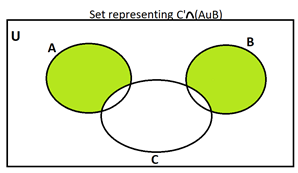
Hence, the shaded region shows $C' \cap \left( {A \cup B} \right)$.
(A) (ii) We have to shade the region represented by $\left( {A \cap B} \right) \cup \left( {B \cap C} \right)$. We can observe in the figure that the set A and the set B are disjoint sets and hence, they have nothing common in them. $\left( {A \cap B} \right) = \varphi$. We will shade the region represented by $\left( {B \cap C} \right)$.

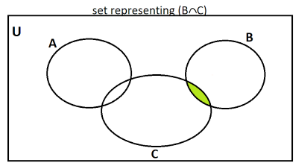
Now our question has become, $\varphi \cup (B \cap C)$. The union of phi and $\left( {B \cap C} \right)$ will include the following region:

Therefore, the shaded region shows $\left( {A \cap B} \right) \cup \left( {B \cap C} \right)$.
(B) (i) we are given $n(A) = 10,n(B) = 7,n({\text{only }}C) = 15$ and we have been asked the value of $n\left( {A \cap B} \right)$.
As we can see in the figure, there is nothing common in the set of A and B.
Therefore, $n\left( {A \cap B} \right)$ $= 0$
(ii) we are given $n(A) = 10,n(B) = 7,n({\text{only }}C) = 15$ and we have been asked the value of $n\left( {A \cup B} \right)$.
$n(A \cup B) = n(A) + n(B) - n(A \cap B)$
Putting all the values,
$n\left( {A \cap B} \right) = 10 + 7 - 0 = 17$
Hence,
$\therefore n\left( {A \cup B} \right) = 17$

Note: A Venn diagram, also called primary diagram, set diagram or logic diagram, is a diagram that shows all possible logical relations between a finite collection of different sets. These diagrams depict elements as points in the plane, and sets as regions inside closed curves. A Venn diagram consists of multiple overlapping closed curves, usually circles, each representing a set.
In part (A) (i), we looked at the common area between two figures because they had the sign of intersection - $' \cap '$between them. This sign means the elements which are common in both the sets.
In part (B) (ii), we did not look at the common area because it had the sign of union - $' \cup '$ between them. This sign includes the elements in both the sets together, and not only common sets.