Question

Consider the following statements:
Statement I The area bounded by the curves ${{y}^{2}}=4{{a}^{2}}(x-1)$ and lines $x=1$ and $y=4a$ is $\dfrac{8a}{3}$ sq. units.
Statement II The area enclosed between the parabola $y={{x}^{2}}-x+2$ and the line $y=x+2$ is $\dfrac{8}{3}$ sq. units.
Choose the correct option.
A. statement I is true
B. statement II is true
C. both statements are true
D. both statements are false

Answer 1

Hint: For verifying statement I, relate the equation of parabola given with the standard equation of the parabola i.e. ${{\left( y-{{y}_{1}} \right)}^{2}}=4a\left( x-{{x}_{1}} \right)$ where $\left( {{x}_{1}},{{y}_{1}} \right)$ is the vertex of the parabola.
For verifying statement II, relate the equation of parabola with the standard equation of parabola i.e. ${{\left( x-{{x}_{1}} \right)}^{2}}=4a\left( y-{{y}_{1}} \right)$, where $\left( {{x}_{1}},{{y}_{1}} \right)$ is the center of the parabola and parabola will be symmetric about the y-axis.
Area of any curve f(x) with the x-axis from x = a to x = b can be given as $\int\limits_{a}^{b}{f(x)}dx$ and similarly area of any curve with the y-axis can also be found.

Complete step-by-step answer:
Statement I: Here, we have curves ${{y}^{2}}=4{{a}^{2}}(x-1)$, $x=1$ and $y=4a$ and hence we need to determine the area bounded by the curves and have to verify with the given area i.e. $\dfrac{8a}{3}$ square units.
Lines x = 1 and y = 4a are the lines parallel to y-axis and x-axis and will pass through (1, 0) and (0, 4a) respectively.
Equation of curve ${{y}^{2}}=4{{a}^{2}}(x-1)$ can be compared with the standard equation of parabola i.e. ${{y}^{2}}=4ax$, which is symmetric about x-axis. As we know vertex of ${{y}^{2}}=4ax$is given as (0, 0) by writing it as ${{\left( y-0 \right)}^{2}}=4a\left( x-0 \right)$. So in a similar approach any parabola of type ${{\left( y-{{y}_{1}} \right)}^{2}}=4a\left( x-{{x}_{1}} \right)$ will have center as $\left( {{x}_{1}},{{y}_{1}} \right)$. So the given equation of parabola can be re-written as,
${{(y-0)}^{2}}=4{{a}^{2}}(x-1)......(1)$
Hence, the center (vertex) of this parabola will be (1,0) and the parabola will be symmetric about the x-axis. So we can draw curves on the coordinate axes as:-

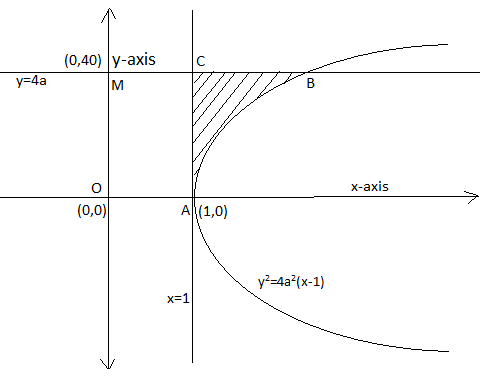
Hence the bounded region is represented in the diagram with shaded part and named as ABCA.
Now let us find point B i.e. intersection of y = 4a and ${{y}^{2}}=4{{a}^{2}}(x-1)$.
So we have,

& y=4a......(2) \\\ & {{y}^{2}}=4{{a}^{2}}(x-1)......(3) \\\ \end{aligned}$$ Put y = 4a in the equation (3) from the equation (2) and hence we get, $$\begin{aligned} & {{\left( 4a \right)}^{2}}=4{{a}^{2}}(x-1) \\\ & 16{{a}^{2}}=4{{a}^{2}}(x-1) \\\ & 4=x-1 \\\ & x=5 \\\ \end{aligned}$$ Hence point B is given as (5, 4a). So length AC can be given. Now we can find the area of the shaded region by calculating the difference of the area of OABMO and OACMO. As we know, the area of any curve f(x) under the x-axis from x = a to b can be given as $$\int\limits_{a}^{b}{f(x)}dx$$. Similarly we can define the function in terms of ‘y’ and get area under the y-axis from y = a to b is given as, $$\int\limits_{a}^{b}{f(y)}dy.....(4)$$ So the area of OABMO can be calculated by integrating the given function in terms of ‘y’ from y = 0 to 4a. An area of OACMO can be calculated by the area of the rectangle. We know, Area of rectangle = $$length\times breadth......(5)$$ So we get the area of shaded region as, Area of shaded region = area of OABMO – area of OACMO……(6) Now, we know the equation of parabola is $$\begin{aligned} & {{y}^{2}}=4{{a}^{2}}(x-1) \\\ & x-1=\dfrac{{{y}^{2}}}{4{{a}^{2}}} \\\ & f(y)=x=\left( \dfrac{{{y}^{2}}}{4{{a}^{2}}}+1 \right)......(7) \\\ \end{aligned}$$ Now we can calculate area of shaded region as, Area of shaded region, $$\begin{aligned} & =\int\limits_{0}^{4a}{\left( \dfrac{{{y}^{2}}}{4{{a}^{2}}}+1 \right)}dy-\left( 1\times 4a \right) \\\ & =\int\limits_{0}^{4a}{\dfrac{{{y}^{2}}}{4{{a}^{2}}}dy+\int\limits_{0}^{4a}{1dy}}-4a \\\ & =\dfrac{1}{4{{a}^{2}}}\int\limits_{0}^{4a}{{{y}^{2}}dy}+\int\limits_{0}^{4a}{1dy}-4a \\\ \end{aligned}$$ We know $$\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}......(8)$$ So we get, Area of shaded region, $$\begin{aligned} & =\dfrac{1}{4a}\left( \dfrac{{{y}^{3}}}{3} \right)_{0}^{4a}+\left( y \right)_{0}^{4a}-4a \\\ & =\dfrac{1}{4{{a}^{2}}}\left[ \dfrac{{{\left( 4a \right)}^{3}}}{3}-0 \right]+\left( 4a-0 \right)-4a \\\ & =\dfrac{64{{a}^{3}}}{12{{a}^{2}}}+4a-4a \\\ \end{aligned}$$ Area of the shaded region $$=\dfrac{16a}{3}$$ sq. units Hence statement I is not correct. Statement II: So here, we have curves $$y={{x}^{2}}-x+2$$ and $$y=x+2$$ and we need to determine the area bounded by the given curves. As $$y=x+2$$ is a straight line with slope 1 (compare with the line y = mx + c where m is slope and c is the intercept). And we can rewrite equation $$y={{x}^{2}}-x+2$$ as, $$\begin{aligned} & y={{x}^{2}}-x+2 \\\ & y={{\left( x-\dfrac{1}{2} \right)}^{2}}-{{\left( \dfrac{1}{2} \right)}^{2}}+2 \\\ & y={{\left( x-\dfrac{1}{2} \right)}^{2}}+2-\dfrac{1}{4} \\\ & \left( y-\dfrac{7}{4} \right)={{\left( x-\dfrac{1}{2} \right)}^{2}}......(9) \\\ \end{aligned}$$ Now we can compare this equation with the parabola, $${{\left( x-{{x}_{1}} \right)}^{2}}=4a\left( y-{{y}_{1}} \right)......(10)$$ where $$\left( {{x}_{1}},{{y}_{1}} \right)$$ is the center/ vertex of the parabola and is symmetric about y-axis (positive y-axis). Hence we get the center of parabola in equation (9) as $$\left( \dfrac{1}{2},\dfrac{7}{4} \right)$$. Hence we can draw the curves on the coordinate axis as,  So we get, Area of the shaded region = area of OATBMO – area of OARBMO….(11) Let us calculate the intersection points of parabola and the straight line given in the problem. So we have, $$\begin{aligned} & y={{x}^{2}}-x+2.....(10) \\\ & y=x+2.......(11) \\\ \end{aligned}$$ Put $$y=x+2$$ from equation (11) to the equation (10). So we get, $$\begin{aligned} & x+2={{x}^{2}}-x+2 \\\ & x={{x}^{2}}-x \\\ & {{x}^{2}}-2x=0 \\\ & x(x-2)=0 \\\ \end{aligned}$$ $$x=0$$ or $$\begin{aligned} & x-2=0 \\\ & x=2 \\\ \end{aligned}$$ Now put x = 0 to the equation (11). We get, $$\begin{aligned} & y=0+2=2 \\\ & y=2 \\\ \end{aligned}$$ And put x = 2 to the equation (11). We get, $$\begin{aligned} & y=2+2=4 \\\ & y=4 \\\ \end{aligned}$$ Hence we get the point of intersections of parabola and straight line are (0, 2) and (2, 4). Hence from the diagram, we get point A and B as (0, 2) and (2, 4) respectively. Hence, line segment OA can be represented as x = 0 and line segment BM is represented as x = 2. Now as we can observe that the region OATBMO is forming a trapezium. So we know, Area of trapezium = $$\dfrac{1}{2}$$ sum of parallel sides $$\times $$ height. So we know, OA = 2, BM = 4, OM =2. So we get, Area of OATBMO = $$\dfrac{1}{2}(4+2)\times 2=6$$ square units. Now the area of region OARBMO can be calculated by integrating the curve in terms of ‘x’ from $$x=0$$ to $$x=2$$. So we get, Area of OARBMO $$=\int\limits_{0}^{2}{\left( {{x}^{2}}-x+2 \right)dx}$$ We know, $$\int{{{x}^{n}}dx=\dfrac{{{x}^{n+1}}}{n+1}}$$. So we get, Area of OARBMO, $$\begin{aligned} & =\int\limits_{0}^{2}{{{x}^{2}}dx}-\int\limits_{0}^{2}{xdx}+2\int\limits_{0}^{2}{1dx} \\\ & =\left( \dfrac{{{x}^{3}}}{3} \right)_{0}^{2}-\left( \dfrac{{{x}^{2}}}{2} \right)_{0}^{2}+2\left( x \right)_{0}^{2} \\\ & =\left( \dfrac{{{2}^{3}}}{3}-0 \right)-\left( \dfrac{{{2}^{2}}}{2}-0 \right)+2\left( 2-0 \right) \\\ & =\dfrac{8}{3}-\dfrac{4}{2}+4=\dfrac{8}{3}+2 \\\ \end{aligned}$$ $$=\dfrac{14}{3}$$ square units Hence, area of shaded region $$=6-\dfrac{14}{3}=\dfrac{4}{3}$$ square units. Hence statement II is also incorrect. So option D (both statements are incorrect and false) is the correct answer. Note: One may calculate the bounded area w.r.t x-axis as well.  Area w.r.t. x-axis can be given as, Area of shaded region = area of ANBCA – area of ABNA where, area of ABNA $$=\int\limits_{0}^{5}{2a\sqrt{x-1}dx}$$ Similarly, the area of the shaded region in the second statement can be calculated w.r.t. y-axis. But here, we need to find the value of ‘x’ from the equation of curve as, $$\begin{aligned} & y={{x}^{2}}-x+2 \\\ & y={{\left( x-\dfrac{1}{2} \right)}^{2}}+\dfrac{7}{4} \\\ & {{\left( x-\dfrac{1}{2} \right)}^{2}}=\left( y-\dfrac{7}{4} \right) \\\ & x=\sqrt{y-\dfrac{7}{4}}+\dfrac{1}{2} \\\ \end{aligned}$$ So it can be another approach for finding the area. Mathematical calculation is an important part of the problem. So take care of it as well.