Question
Question: Consider the following statements: I. $\lim_{n \to \infty} \frac{2^n + (-2)^n}{2^n}$ does not exist...
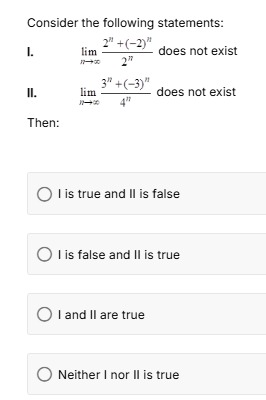
Consider the following statements:
I. limn→∞2n2n+(−2)n does not exist
II. limn→∞4n3n+(−3)n does not exist
Then:
I is true and II is false
I is false and II is true
Both I and II are true
Both I and II are false
I is true and II is false
Solution
To analyze the statements, we evaluate each limit separately.
Statement I: limn→∞2n2n+(−2)n does not exist.
Let's simplify the expression: 2n2n+(−2)n=2n2n+2n(−2)n=1+(2−2)n=1+(−1)n
Now, consider the behavior of 1+(−1)n as n→∞:
- If n is an even integer (e.g., n=2,4,6,…), then (−1)n=1. So, 1+(−1)n=1+1=2.
- If n is an odd integer (e.g., n=1,3,5,…), then (−1)n=−1. So, 1+(−1)n=1−1=0.
Since the expression oscillates between two different values (2 and 0) as n→∞, the limit does not exist. Therefore, Statement I is true.
Statement II: limn→∞4n3n+(−3)n does not exist.
Let's analyze the expression 4n3n+(−3)n.
-
If n is an even integer (let n=2k for some integer k≥1): 42k32k+(−3)2k=42k32k+32k=42k2⋅32k=2(4232)k=2(169)k As n→∞, k→∞. Since 169<1, we know that limk→∞(169)k=0. Thus, limn→∞,n even4n3n+(−3)n=2⋅0=0.
-
If n is an odd integer (let n=2k+1 for some integer k≥0): 42k+132k+1+(−3)2k+1=42k+132k+1−32k+1=42k+10=0 As n→∞, the value of the expression is always 0. Thus, limn→∞,n odd4n3n+(−3)n=0.
Since the limit approaches the same value (0) for both even and odd values of n, the limit limn→∞4n3n+(−3)n exists and is equal to 0. Therefore, Statement II, which claims the limit does not exist, is false.
Conclusion: Statement I is true. Statement II is false.
