Question

Consider the following statements :
1. The magnitude of $\overrightarrow {\text{a}} {\text{ }} \times {\text{ }}\overrightarrow {\text{b}}$ is same as the area of a triangle with sides a and b
2. If $\overrightarrow {\text{a}} {\text{ }} \times {\text{ }}\overrightarrow {\text{b}} = 0$ where $\overrightarrow {\text{a}} {\text{ }} \ne {\text{0}}$, $\overrightarrow {\text{b}} {\text{ }} \ne {\text{0}}$ then $\overrightarrow {\text{a}} {\text{ = }}\lambda \overrightarrow {\text{b}}$
Which of the above statements is/are correct ?
A .1 only
B .2 only
C. Both 1 and 2
D. Neither 1 nor 2

Answer 1

Hint: Proceed the solution of this question with the knowledge that magnitude of a × b gives the area of parallelogram and if the cross product of two vectors is zero then they will be parallel or collinear.

Complete step-by-step answer:
We know that
Cross product of two three-dimensional vectors a and b i.e. a × b is a vector that is perpendicular to both a and b.

$\Rightarrow \left| {\overrightarrow {\text{a}} {\text{ }} \times {\text{ }}\overrightarrow {\text{b}} } \right|$ is the area of the parallelogram formed by the vector $\overrightarrow {\text{a}} {\text{ and }}\overrightarrow {\text{b}}$.
In other words $\left| {\overrightarrow {\text{a}} {\text{ }} \times {\text{ }}\overrightarrow {\text{b}} } \right|$ is the area of the parallelogram whose adjacent sides are the vectors $\overrightarrow {\text{a}} {\text{ and }}\overrightarrow {\text{b}}$
From simple trigonometry, we can prove this thing-

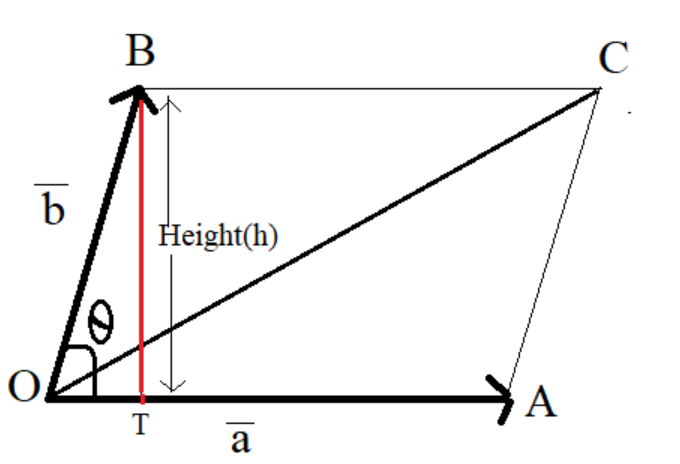
So in given figure, Δ OBT is a right angle triangle whose perpendicular length is the height of parallelogram OACB
We know that, Area of parallelogram = base × height
In the figure, base OA = $\left| {\overrightarrow {{\text{ a}}} {\text{ }}} \right|$
Height BT = $\left| {\overrightarrow {{\text{ b}}} {\text{ }}} \right|{\text{sin}}\theta$
Area of parallelogram = base × height= $\left| {\overrightarrow {{\text{ a}}} {\text{ }}} \right|$ $\left| {\overrightarrow {{\text{ b}}} {\text{ }}} \right|{\text{sin}}\theta$……..(1)
where θ is the angle between the vector $\overrightarrow {\text{a}} {\text{ and }}\overrightarrow {\text{b}}$.

And from vector calculus we know that $\left| {\overrightarrow {\text{a}} {\text{ }} \times {\text{ }}\overrightarrow {\text{b}} } \right| = \left| {\overrightarrow {\text{a}} } \right| \times \left| {{\text{ }}\overrightarrow {\text{b}} } \right|{\text{sin}}\theta$…….(2)
Hence by equation (1) & (2)
It has been prove that $\Rightarrow \left| {\overrightarrow {\text{a}} {\text{ }} \times {\text{ }}\overrightarrow {\text{b}} } \right|$ is the area of the parallelogram
$\Rightarrow \left| {\overrightarrow {\text{a}} {\text{ }} \times {\text{ }}\overrightarrow {\text{b}} } \right|$ = Area of parallelogram with sides a and b
Hence The first statement is wrong, the magnitude of cross product of 2 vectors represents area of Parallelogram not triangle.
We now that
If the cross product of two vectors are zero vectors if both the vectors are parallel or opposite to each other. Conversely, if two vectors are parallel or opposite to each other, then their product is a zero vector. Two vectors have the same sense of direction.

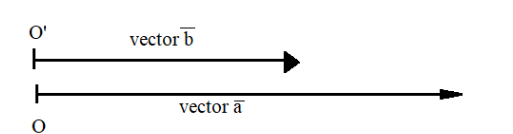
So in the above figure, vectors $\overrightarrow {\text{a}} {\text{ and }}\overrightarrow {\text{b}}$ are parallel and angle between them will be zero.

$\Rightarrow \overrightarrow {\text{a}} {\text{ }} \times {\text{ }}\overrightarrow {\text{b}} = \left| {\overrightarrow {\text{a}} } \right| \times \left| {{\text{ }}\overrightarrow {\text{b}} } \right|{\text{sin}}\theta = 0$
$\because \left| {\overrightarrow {\text{a}} } \right| \ne 0,{\text{ }}\left| {{\text{ }}\overrightarrow {\text{b}} } \right| \ne 0{\text{ }} \Rightarrow {\text{ }}\theta = 0$
Hence we can write one vector as a linear combination of other vectors.
⇒$\because \overrightarrow {\text{a}} {\text{ }} \times {\text{ }}\overrightarrow {\text{b}} = 0 \Rightarrow \overrightarrow {\text{a}} {\text{ || }}\overrightarrow {\text{b}}$
∴a=λb
Hence The second statement is true as cross product is 0 and magnitude of vector A and B is not zero implies sinX=0 i.e. angle between them is 0 implies they are collinear
Hence from the given option, B is correct.

Note: In this particular question we should know that the magnitude of the cross product is largest when vector $\overrightarrow {\text{a}} {\text{ and }}\overrightarrow {\text{b}}$ are perpendicular. On the other hand, if vector $\overrightarrow {\text{a}} {\text{ and }}\overrightarrow {\text{b}}$are parallel or if either vector is the zero vector, then the cross product is the zero vector. If the vectors are parallel or one vector is the zero vector, then there is not a unique line perpendicular to both vector $\overrightarrow {\text{a}} {\text{ and }}\overrightarrow {\text{b}}$. But since there is only one vector of zero length, the definition still uniquely determines the cross product.In vectors collinear or parallel both are the same thing because vectors have the property to shift along it.