Question

Consider the following linear programming problem
Maximize $12X+10Y$
Subject to: $\begin{aligned} & 4X+3Y\le 480 \\\ & 2X+3Y\le 360 \\\ \end{aligned}$
All variables $\ge 0$
which of the following points$\left( X,Y \right)$ could be a feasible corner point?
A. $\left( 40,48 \right)$
B. $\left( 120,0 \right)$
C. $\left( 180,120 \right)$
D. $\left( 30,36 \right)$
E. None of the above

Answer 1

On the x-axis the value of Y is equal to zero similarly using this concept by putting the values of X and Y as zeros in the equation we have to generate points on the coordinate axis. By substituting the values we can maximize the given expression.

Complete step by step answer:

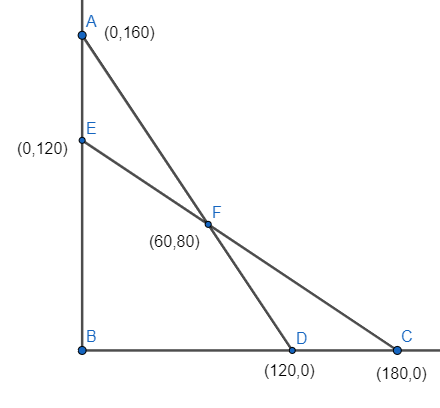
Consider the given equation $4X+3Y\le 480$
$4X+3Y=480$
By putting the values of x and y as zeros we get the points on x and y axis as,
When x is zero the value of y is 160 that means $(0,160)$ is the Point A
When y is zero the value of x is 120 that means $\left( 120,0 \right)$ is the Point D
Now consider the given equation $2X+3Y\le 360$
$2X+3Y=360$
When x is zero the value of y is 120 that means $\left( 0,120 \right)$is the Point E
When y is zero the value of x is 180 that means $\left( 180,0 \right)$is the Point C
By subtracting the given equations $4X+3Y\le 480$ and $2X+3Y\le 360$ we get,

& 4X+3Y=480 \\\ & \underline{2X+3Y=360} \\\ & 2X\,\,\,\,\,\,\,\,\,\,\,\,\,\,=120 \\\ & \,\,\,X\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\,\,\,\,60\,\,\,\,\, \\\ \end{aligned}$$ On substituting $$X=60$$ in equation $$2X+3Y=360$$ and solving we get, $$\begin{aligned} & 2\left( 60 \right)+3Y=360 \\\ & 3Y=360-120 \\\ & Y=\dfrac{240}{3} \\\ & Y=80 \end{aligned}$$ The intersection of these two lines we get a point as (60,80) which is the Point F F (60,80) If we plot all the points and lines on coordinate axis then we can conclude the feasible corner points as $$\left( 0,120 \right)$$,$$\left( 120,0 \right)$$ $$\left( 120,0 \right)$$ is the feasible corner point. **So, the correct answer is “Option B”.** **Note:** The feasible corner points are the points formed by the lines on the coordinate axis in the feasible region. From the plot we can conclude that in the feasible region these two points are the feasible corner points.