Question
Question: Consider the following Galvanic cell. By what value does the cell voltage change when concentration ...
Consider the following Galvanic cell. By what value does the cell voltage change when concentration of ions in the anodic and cathodic compartment both increase by a factor of 10 at 298K?
(A)+0.0591
(B)−0.0591
(C)−0.1182
(D)0
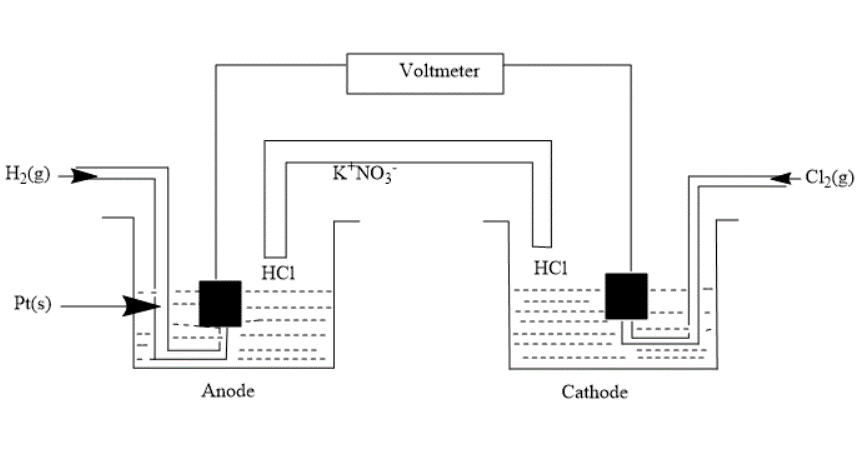
Solution
To solve the question we have to first look carefully at the galvanic cell and then write the cathode and anode reactions. After this, we will be using the Nernst Equation to get the final result. Nernst Equation is an important equation in electrochemistry used to calculate the cell potential at a particular temperature, pressure, or concentration.
Complete Step By Step Answer:
The following is how the Nernst equation is expressed-
E=E∘−nF2.303RTlog[R][P]−−−(1)
Where E is cell potential
E∘ is the standard cell potential
F is Faraday’s constant and its value is 96500 C/mole
n is the number of electrons transferred
T is the temperature in Kelvin
R is gas constant and its value is 8.314J/moleK
[P] and [R] are the product and reactant concentration respectively.
At temperature 25 °C (or 298 K) the equation (1) can be modified as under-
E=E∘−n0.0591log[R][P]−−−(2)
(Here we simply place all the values like T=298K, F=96500 C/mol, and R=8.314J/moleK)
In the question, we are given a galvanic cell i.e. an electrochemical cell that converts chemical energy into electrical energy.
First, we write the half-cell reactions-
Anode- H2(g)→2H+(aq.)+2e− (Oxidation)
Cathode- Cl2(g)+2e−→2Cl−(aq.) (Reduction)
Overall cell reaction will be- H2(g)+Cl2(g)→2H+(aq.)+2Cl−(aq.)−−−(3)
So the value of n will be 2(number of electrons transferred in redox reaction).
Writing Nernst equation for the equation (3) we will get-
⇒E=E∘−20.0591logpH2pCl2[H+]2[Cl−]2−−−(4)
(Here we consider the pressure of Hydrogen and chlorine gases in the reactant part)
Now in the question, we are specified that we increase the concentration terms by a factor of 10, so making the necessary replacements we have-
⇒E=E∘−20.0591logpH2pCl2[10×H+]2[10×Cl−]2−−−(5)
The equation on solving further becomes-
⇒E=E∘−20.0591logpH2pCl2100[H+]2×100[Cl−]2−−−(6)
⇒E=E∘−20.0591logpH2pCl210000×[H+]2[Cl−]2−−−(7)
Simplifying the equation using, logAB=logA+logB we get-
⇒E=E∘−20.0591[logpH2pCl2[H+]2[Cl−]2+log10000]−−−(8)
So equation (8) becomes,
⇒E=E∘−20.0591logpH2pCl2[H+]2[Cl−]2−20.0591log104−−−(9)
As we know log 10000 can be written as log 104 which is equal to 4 since log 10 is 1.
⇒E=E∘−20.0591logpH2pCl2[H+]2[Cl−]2−20.0591×4−−−(10)
⇒E=E∘−20.0591logpH2pCl2[H+]2[Cl−]2−0.1182−−−(11)
In the question, we are asked to calculate the change so we find it by subtracting equation (11) from equation (4)-
⇒ΔE=E∘−20.0591logpH2pCl2[H+]2[Cl−]2−20.0591logpH2pCl2[H+]2[Cl−]2−0.1182−−−(12)
⇒ΔE=−0.1182V
So option(C) is correct.
Note:
Apart from the calculation of cell potential using the Nernst equation one can also calculate other such quantities like pH, Solubility product, Equilibrium constant, and some thermodynamic quantities like Gibbs free energy. It has huge applications in potentiometric titrations and finding unknown ionic concentrations.
