Question

Consider the expression $4{{\lambda }^{2}}-5{{\mu }^{2}}+6\lambda +1=0$ . If $\lambda x+\mu y+1=0$ touches a definite circle, then centre and radius will be
(a) $\left( 3,0 \right)$ and $\sqrt{5}$
(b) $\left( -3,0 \right)$ and $\sqrt{7}$
(c) $\left( 0,3 \right)$ and $\sqrt{5}$
(d) None of these.

Answer 1

Here we will use the distance formula given by, $d=\dfrac{\left| a{{x}_{0}}+b{{y}_{0}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$, because the equation of the line touches the circle as a tangent and the equation of the tangent is $a{{x}_{0}}+b{{y}_{0}}+c$. Here tangent $a{{x}_{0}}+b{{y}_{0}}+c$ is given as $\lambda x+\mu y+1$ in this question. The distance d is actually the distance between the equation of tangent $\lambda x+\mu y+1=0$ and the centre of the circle. With the help of these we will solve the question.

Complete step-by-step answer :
The equation of the family of circles is given by the formula ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$. We will first consider the diagram for this question.

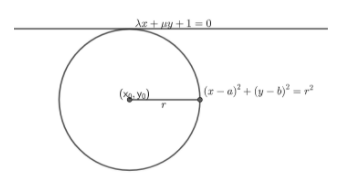
In this diagram, r is the radius of the circle and the points, $\left( {{x}_{0}},{{y}_{0}} \right)$ are the points of its centre. The tangent $\lambda x+\mu y+1=0$ passes through the circle.
We know that the distance of the centre of the circle to the tangent is equal to the radius of the circle. From this fact, we can use the distance formula from the centre of the circle $\left( {{x}_{0}},{{y}_{0}} \right)$ to the tangent. Since, equation of line touches the circle as a tangent is given as $\lambda x+\mu y+1=0$, so the distance formula will be, $d=\dfrac{\left| \lambda x+\mu y+1 \right|}{\sqrt{{{\lambda }^{2}}+{{\mu }^{2}}}}$. Here, d is the distance from the centre of the circle to the line of the tangent. Also, we know that this distance is equal to the radius of the circle, so we can write as,
$r=\dfrac{\left| \lambda x+\mu y+1 \right|}{\sqrt{{{\lambda }^{2}}+{{\mu }^{2}}}}$. We consider $\left| \lambda x+\mu y+1 \right|$ as positive, so $\left| \lambda x+\mu y+1 \right|=\left( \lambda x+\mu y+1 \right)$. And this equation touches the circle with an equation in the form of ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$. So, we can write x = a and y = b. Therefore, we get the terms as, $\lambda a+\mu b+1$. Now we will multiply both sides of the distance formula by $\sqrt{{{\lambda }^{2}}+{{\mu }^{2}}}$. So, we get,
$r=\dfrac{\lambda a+\mu b+1}{\sqrt{{{\lambda }^{2}}+{{\mu }^{2}}}}$
$\Rightarrow r\sqrt{{{\lambda }^{2}}+{{\mu }^{2}}}=\lambda a+\mu b+1$
Now, we will square the equation on both the sides. So, we get,
${{\left( r\sqrt{{{\lambda }^{2}}+{{\mu }^{2}}} \right)}^{2}}={{\left( \lambda a+\mu b+1 \right)}^{2}}$
Now we will apply the formula ${{\left( x+y+z \right)}^{2}}={{x}^{2}}+{{y}^{2}}+{{z}^{2}}+2xy+2yz+2xz$ to the right hand side of the above equation. So, we get,
${{r}^{2}}\left( {{\lambda }^{2}}+{{\mu }^{2}} \right)={{\lambda }^{2}}{{a}^{2}}+{{\mu }^{2}}{{b}^{2}}+2\lambda a\mu b+2\lambda a+2\mu b+1$
$\Rightarrow {{r}^{2}}{{\lambda }^{2}}+{{r}^{2}}{{\mu }^{2}}={{\lambda }^{2}}{{a}^{2}}+{{\mu }^{2}}{{b}^{2}}+2\lambda a\mu b+2\lambda a+2\mu b+1$
$\Rightarrow -{{r}^{2}}{{\lambda }^{2}}+{{\lambda }^{2}}{{a}^{2}}-{{r}^{2}}{{\mu }^{2}}+{{\mu }^{2}}{{b}^{2}}+2\lambda a\mu b+2\lambda a+2\mu b+1=0$
Now, we take the common terms ${{\lambda }^{2}}$ and ${{\mu }^{2}}$, we get,
${{\lambda }^{2}}\left( {{a}^{2}}-{{r}^{2}} \right)+{{\mu }^{2}}\left( {{b}^{2}}-{{r}^{2}} \right)+2\lambda a\mu b+2\lambda a+2\mu b+1=0\ldots \ldots \ldots \left( i \right)$
Let us consider the expression given in the question as,
$4{{\lambda }^{2}}-5\mu +6\lambda +1=0\ldots \ldots \ldots \left( ii \right)$
Now, from equations (i) and (ii), we get,
$\dfrac{{{a}^{2}}-{{r}^{2}}}{4}=\dfrac{{{b}^{2}}-{{r}^{2}}}{-5}=\dfrac{2ab}{0}=\dfrac{2a}{6}=\dfrac{2b}{0}=1$
By equating the variables with constant 1, we get the pairs as,
$\dfrac{{{a}^{2}}-{{r}^{2}}}{4}=1,\dfrac{{{b}^{2}}-{{r}^{2}}}{-5}=1,\dfrac{2a}{6}=1$
We can write these three equations as,
$\begin{aligned} & {{a}^{2}}-{{r}^{2}}=4\ldots \ldots \ldots \left( iii \right) \\\ & {{b}^{2}}-{{r}^{2}}=-5\ldots \ldots \ldots \left( iv \right) \\\ & \dfrac{2a}{6}=1 \\\ \end{aligned}$
We will first solve $\dfrac{2a}{6}=1\Rightarrow 2a=6\Rightarrow a=3$. Now we will solve equations (iii) and (iv) by subtracting them as,
$\begin{aligned} & {{a}^{2}}-{{r}^{2}}=4 \\\ & \dfrac{{{b}^{2}}-{{r}^{2}}=-5}{{{a}^{2}}-{{b}^{2}}=9} \\\ \end{aligned}$
Now, we will put the value of a = 3 in the above equation, so we get,
${{\left( 3 \right)}^{2}}-{{b}^{2}}=9\Rightarrow 9=9+{{b}^{2}}\Rightarrow 9-9={{b}^{2}}\Rightarrow b=0$
We will further substitute the value of b in equation (iv) to get the value of r. So, we get,
${{\left( 0 \right)}^{2}}-{{r}^{2}}=-5\Rightarrow r=\sqrt{5}$
We will now substitute the values of a, b and r in the equation of the circle ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$.And we get, ${{\left( x-3 \right)}^{2}}+{{\left( y-0 \right)}^{2}}=5\Rightarrow {{\left( x-3 \right)}^{2}}+{{y}^{2}}=5$.
Hence we get the answer as $\left( 3,0 \right)$ and $\sqrt{5}$. Therefore, the correct answer is option A.

Note :While comparing equation (i) and (ii), remember that you can alternatively compare ${{a}^{2}}-{{r}^{2}}=4$ directly and so also the other terms in equations (i) and (ii). The equation of the tangent $\lambda x+\mu y+1=0$ has been taken out of the modulus because the use of modulus implies a positive value. Since the values are not given, we can do this default step of writing $\left| \lambda x+\mu y+1 \right|$ as $\lambda x+\mu y+1$. As we need to find the radius therefore, the distance formula works better here. This is due to the fact that the radius is actually the distance between the centre of the circle and the tangent $\lambda x+\mu y+1=0$.