Question

Consider the equation $|x-2|-|x+1|=k$.

If the equation has exactly one solution, then find the number of integral values of $k$.

Answer 1

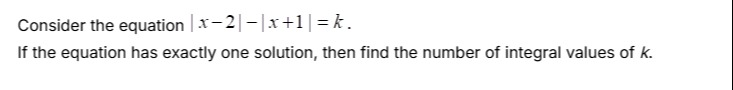
5

Answer 2

The given equation is $|x-2|-|x+1|=k$. Let $f(x) = |x-2|-|x+1|$. We need to find the values of $k$ for which the equation $f(x)=k$ has exactly one solution. We analyze the function $f(x)$ by considering the intervals defined by the critical points $x=2$ and $x=-1$.

Case 1: $x \le -1$ In this interval, $x-2 \le -3 < 0$ and $x+1 \le 0$. $|x-2| = -(x-2) = 2-x$ $|x+1| = -(x+1) = -x-1$ $f(x) = (2-x) - (-x-1) = 2-x+x+1 = 3$. So, for $x \le -1$, $f(x) = 3$.

Case 2: $-1 < x \le 2$ In this interval, $x-2 \le 0$ and $x+1 > 0$. $|x-2| = -(x-2) = 2-x$ $|x+1| = x+1$ $f(x) = (2-x) - (x+1) = 2-x-x-1 = 1-2x$. For $x=-1$, $f(-1) = 1-2(-1) = 3$. For $x=2$, $f(2) = 1-2(2) = -3$.

Case 3: $x > 2$ In this interval, $x-2 > 0$ and $x+1 > 3 > 0$. $|x-2| = x-2$ $|x+1| = x+1$ $f(x) = (x-2) - (x+1) = x-2-x-1 = -3$. So, for $x > 2$, $f(x) = -3$.

Summarizing the function $f(x)$: $f(x) = \begin{cases} 3 & \text{if } x \le -1 \\ 1-2x & \text{if } -1 < x \le 2 \\ -3 & \text{if } x > 2 \end{cases}$

We are looking for the values of $k$ such that $f(x)=k$ has exactly one solution. Let's analyze the number of solutions for different values of $k$:

• If $k > 3$: The horizontal line $y=k$ is above the maximum value of $f(x)$. There are no solutions.
• If $k = 3$: The equation is $f(x)=3$. From the definition of $f(x)$, $f(x)=3$ for all $x \le -1$. This gives infinitely many solutions.
• If $-3 < k < 3$: The equation is $f(x)=k$.
  • For $x \le -1$, $f(x)=3$. Since $k < 3$, there are no solutions in this interval.
  • For $-1 < x \le 2$, $f(x)=1-2x$. The equation is $1-2x=k$. This is a linear equation $2x = 1-k$, so $x = (1-k)/2$. Since $-3 < k < 3$, we have $-3 < k < 3 \implies -3 < -k < 3 \implies -2 < 1-k < 4 \implies -1 < (1-k)/2 < 2$. The solution $x=(1-k)/2$ lies in the interval $(-1, 2)$, which is within the case $-1 < x \le 2$. Thus, there is exactly one solution in this interval.
  • For $x > 2$, $f(x)=-3$. Since $k > -3$, there are no solutions in this interval. So, for $-3 < k < 3$, there is exactly one solution.
• If $k = -3$: The equation is $f(x)=-3$.
  • For $x \le -1$, $f(x)=3$. $3=-3$ is false, no solutions.
  • For $-1 < x \le 2$, $f(x)=1-2x$. $1-2x=-3 \implies 2x=4 \implies x=2$. This solution is in the interval $(-1, 2]$. So $x=2$ is a solution.
  • For $x > 2$, $f(x)=-3$. The equation $-3=-3$ holds for all $x > 2$. This gives infinitely many solutions. So, for $k=-3$, the solutions are $x=2$ and all $x > 2$, which is all $x \ge 2$. Infinitely many solutions.
• If $k < -3$: The horizontal line $y=k$ is below the minimum value of $f(x)$. There are no solutions.

The equation $|x-2|-|x+1|=k$ has exactly one solution when $-3 < k < 3$. We need to find the number of integral values of $k$ in the interval $(-3, 3)$. The integers in this interval are $-2, -1, 0, 1, 2$. There are 5 integral values of $k$.

The final answer is $\boxed{5}$.