Question

Consider the equation $(x + 1)(x + 2)(x + 3)... (x + n) = c$ and answer the following:

a) What can be the maximum multiplicity of a root of this equation? b) If n=2025, for how many values of c can this multiplicity be achieved? c) If n=2024, for how many values of c can this multiplicity be achieved?

Answer 1

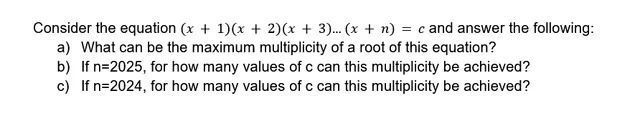
a) 2, b) 2024, c) 1012

Answer 2

The equation is given by $f(x) = (x + 1)(x + 2)...(x + n) = c$. We need to analyze the multiplicity of its roots.

a) Maximum multiplicity of a root:

Let $P(x) = f(x) - c$. If $x_0$ is a root of $P(x)$ with multiplicity $k$, then $P(x_0) = 0$, $P'(x_0) = 0$, ..., $P^{(k-1)}(x_0) = 0$, and $P^{(k)}(x_0) \neq 0$.

Since $c$ is a constant, $P'(x) = f'(x)$, $P''(x) = f''(x)$, and so on.

Thus, if $x_0$ is a root of $P(x)$ with multiplicity $k$, then $x_0$ must be a root of $f'(x)$ with multiplicity $k-1$.

The polynomial $f(x) = (x+1)(x+2)...(x+n)$ has $n$ distinct real roots: $-1, -2, ..., -n$.

By Rolle's Theorem, $f'(x)$ must have $n-1$ distinct real roots, say $\alpha_1 < \alpha_2 < ... < \alpha_{n-1}$. These are the critical points of $f(x)$.

Since all roots of $f'(x)$ are distinct, the maximum multiplicity of any root of $f'(x)$ is 1.

If $x_0$ is a root of $f'(x)$ with multiplicity $k-1$, then $k-1 \le 1$, which implies $k \le 2$.

Therefore, the maximum multiplicity of a root of the equation $(x + 1)(x + 2)...(x + n) = c$ can be 2.

This multiplicity is achieved when $x_0$ is a critical point of $f(x)$ (i.e., $f'(x_0)=0$) and $c = f(x_0)$. In this case, $f(x_0)-c=0$ and $f'(x_0)=0$. Since $f'(x)$ has distinct roots, $f''(x_0) \neq 0$, so $x_0$ is a root of multiplicity 2.

b) If n=2025, for how many values of c can this multiplicity be achieved?

For $n=2025$, the maximum multiplicity is 2. This multiplicity is achieved for values of $c = f(\alpha_i)$, where $\alpha_i$ are the roots of $f'(x)=0$. There are $n-1 = 2025-1 = 2024$ distinct critical points.

Let the roots be $-2025, -2024, ..., -1$.

The critical points $\alpha_i$ are located between consecutive roots of $f(x)$.

The sign of $f(x)$ in the interval $(-k-1, -k)$ is $(-1)^k$.

The critical points are $\alpha_1 < \alpha_2 < ... < \alpha_{2024}$.

• $\alpha_1 \in (-2025, -2024)$. Here $k=2024$, so $f(x) > 0$. $f(\alpha_1)$ is a local maximum ($>0$).
• $\alpha_2 \in (-2024, -2023)$. Here $k=2023$, so $f(x) < 0$. $f(\alpha_2)$ is a local minimum ($<0$).
• $\alpha_3 \in (-2023, -2022)$. Here $k=2022$, so $f(x) > 0$. $f(\alpha_3)$ is a local maximum ($>0$).

In general, $f(\alpha_i)$ is positive if $i$ is odd (local maxima), and $f(\alpha_i)$ is negative if $i$ is even (local minima).

For $n=2025$ (odd):

• Positive local maxima: $f(\alpha_1), f(\alpha_3), ..., f(\alpha_{2023})$. There are $(2023-1)/2 + 1 = 1012$ such values.
• Negative local minima: $f(\alpha_2), f(\alpha_4), ..., f(\alpha_{2024})$. There are $(2024-2)/2 + 1 = 1012$ such values.

Since $n=2025$ is odd, the polynomial $f(x)$ is not symmetric about its mean of roots. (For $f(x)$ to be symmetric, the roots must be symmetric about 0 after a shift, e.g., $x(x^2-a^2)(x^2-b^2)...$, which means $n$ must be odd, and the roots must be of the form $0, \pm r_1, \pm r_2, ...$. Our roots $-1, -2, ..., -n$ are not symmetric about their mean $-(n+1)/2$ for odd $n$, unless $n=1$).

For $n>1$, the values of the extrema are generally distinct. For this type of polynomial, $f(\alpha_i) \neq f(\alpha_j)$ if $i \neq j$, provided they are of the same type (both positive or both negative).

Thus, all $1012$ positive values are distinct, and all $1012$ negative values are distinct.

Since positive values cannot be equal to negative values, all $1012 + 1012 = 2024$ values of $c$ are distinct.

For $n=2025$, the number of values of $c$ for which multiplicity 2 can be achieved is 2024.

c) If n=2024, for how many values of c can this multiplicity be achieved?

For $n=2024$, the maximum multiplicity is 2. This multiplicity is achieved for $c = f(\alpha_i)$, where $\alpha_i$ are the roots of $f'(x)=0$. There are $n-1 = 2024-1 = 2023$ distinct critical points.

Let the roots be $-2024, -2023, ..., -1$.

The critical points are $\alpha_1 < \alpha_2 < ... < \alpha_{2023}$.

The sign of $f(x)$ in the interval $(-k-1, -k)$ is $(-1)^k$.

• $\alpha_1 \in (-2024, -2023)$. Here $k=2023$, so $f(x) < 0$. $f(\alpha_1)$ is a local minimum ($<0$).
• $\alpha_2 \in (-2023, -2022)$. Here $k=2022$, so $f(x) > 0$. $f(\alpha_2)$ is a local maximum ($>0$).
• $\alpha_3 \in (-2022, -2021)$. Here $k=2021$, so $f(x) < 0$. $f(\alpha_3)$ is a local minimum ($<0$).

In general, $f(\alpha_i)$ is negative if $i$ is odd (local minima), and $f(\alpha_i)$ is positive if $i$ is even (local maxima).

For $n=2024$ (even):

• Negative local minima: $f(\alpha_1), f(\alpha_3), ..., f(\alpha_{2023})$. There are $(2023-1)/2 + 1 = 1012$ such values.
• Positive local maxima: $f(\alpha_2), f(\alpha_4), ..., f(\alpha_{2022})$. There are $(2022-2)/2 + 1 = 1011$ such values.

For even $n$, the polynomial $f(x)$ is symmetric about the midpoint of its roots, $-(n+1)/2$.

Let $y = x + (n+1)/2$. Then $f(x)$ becomes $G(y) = (y - (n-1)/2)(y - (n-3)/2)...(y + (n-3)/2)(y + (n-1)/2)$.

This $G(y)$ is an even function of $y$ because it is a product of terms $(y-a_k)(y+a_k) = y^2-a_k^2$. So $G(y) = G(-y)$.

If $y_0$ is a critical point of $G(y)$, then $-y_0$ is also a critical point, and $G(y_0) = G(-y_0)$.

The critical points of $G(y)$ are symmetric about $y=0$.

The values of $y$ for critical points are $y_1, -y_1, y_2, -y_2, ..., y_{(n-2)/2}, -y_{(n-2)/2}$, and $0$. (Total $n-1$ critical points).

For $n=2024$, the number of critical points is $2023$.

The critical points for $y$ are $0, \pm y_1, \pm y_2, ..., \pm y_{1011}$.

$G(0)$ is a local maximum ($>0$). This corresponds to $x = -(n+1)/2 = -2025/2 = -1012.5$. This critical point is $\alpha_{1012}$ (since $1012$ is even, it's a local max).

The values $G(y_i)$ and $G(-y_i)$ are equal. So $f(\alpha_j)$ and $f(\alpha_k)$ will be equal for critical points $\alpha_j$ and $\alpha_k$ that are symmetric about $-(n+1)/2$.

There are $1011$ pairs of symmetric critical points. Each pair gives rise to one distinct value of $c$.

$f(\alpha_1) = f(\alpha_{2023})$, $f(\alpha_3) = f(\alpha_{2021})$, etc.

The values of the local minima are $f(\alpha_1), f(\alpha_3), ..., f(\alpha_{1011})$. These are $1011/2 + 1 = 506$ distinct values. No, it's $(1011-1)/2+1 = 506$ distinct values.

The values of the local minima are $f(\alpha_1), f(\alpha_3), ..., f(\alpha_{2023})$.

Due to symmetry, $f(\alpha_i) = f(\alpha_{n-i})$. So $f(\alpha_1)=f(\alpha_{2023})$, $f(\alpha_3)=f(\alpha_{2021})$, etc.

The distinct negative values are $f(\alpha_1), f(\alpha_3), ..., f(\alpha_{1011})$. There are $(1011-1)/2 + 1 = 506$ such values.

The distinct positive values are $f(\alpha_2), f(\alpha_4), ..., f(\alpha_{2022})$.

The critical point at $y=0$ (i.e. $x=-(n+1)/2$) is $\alpha_{n/2}$. For $n=2024$, this is $\alpha_{1012}$. This is a maximum value.

The values are $f(\alpha_2), f(\alpha_4), ..., f(\alpha_{1010}), f(\alpha_{1012}), f(\alpha_{1014}), ..., f(\alpha_{2022})$.

Due to symmetry, $f(\alpha_i) = f(\alpha_{n-i})$. So $f(\alpha_2)=f(\alpha_{2022})$, $f(\alpha_4)=f(\alpha_{2020})$, etc.

The distinct positive values are $f(\alpha_2), f(\alpha_4), ..., f(\alpha_{1010})$ and $f(\alpha_{1012})$.

There are $(1010-2)/2 + 1 = 505$ values from the symmetric pairs and 1 value from the central critical point. So $505+1=506$ distinct positive values.

Total distinct values of $c$: $506 \text{ (negative)} + 506 \text{ (positive)} = 1012$.

For $n=2024$, the number of values of $c$ for which multiplicity 2 can be achieved is 1012.