Question

Consider the ellipse $\dfrac{{{x}^{2}}}{f({{k}^{2}}+2k+5)}+\dfrac{{{y}^{2}}}{f(k+11)}=1$ , where $f(x)$is a positive decreasing function, then value of $k$ for which major axis coincides with the $x$ axis is :
(a) $k\in (-7,-5)$
(b) $k\in (-5,-3)$
(c) $k\in (-3,2)$
(d) None of these

Answer 1

Hint: In an ellipse the lengths of the major and minor axis are different. The length of the major axis = $2a$ and the length of the minor axis = $2b$, if $a > b$and the length of the major axis = $2b$ and the length of the minor axis = $2a$, if $b > a$.
The general equation of an ellipse is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$. Compare the equation given above with this general equation, and then apply some knowledge of increasing and decreasing functions after satisfying the condition given in the question.

Complete step-by-step solution -
For an ellipse having the general formula :
$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$, the vertex of the ellipse is $(0,0)$.
If $a > b$: the major axis of the ellipse lies on the $x$ axis.
Here is a diagram of what such an ellipse would look like :

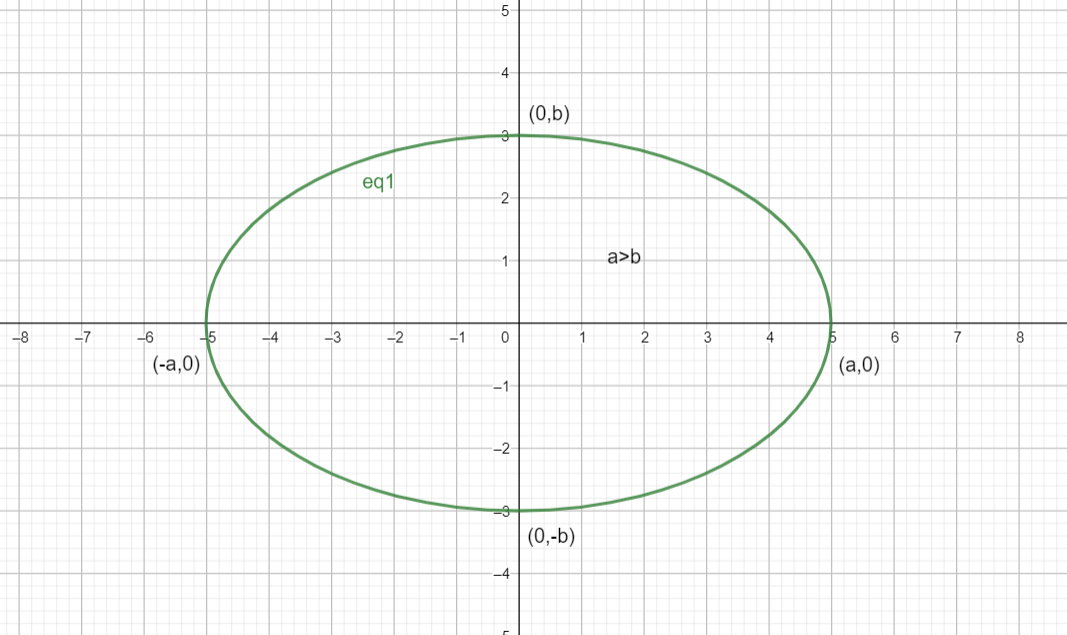
If $b > a$: the major axis of the ellipse lies on the $y$ axis.
Here is a diagram of what such an ellipse would look like :

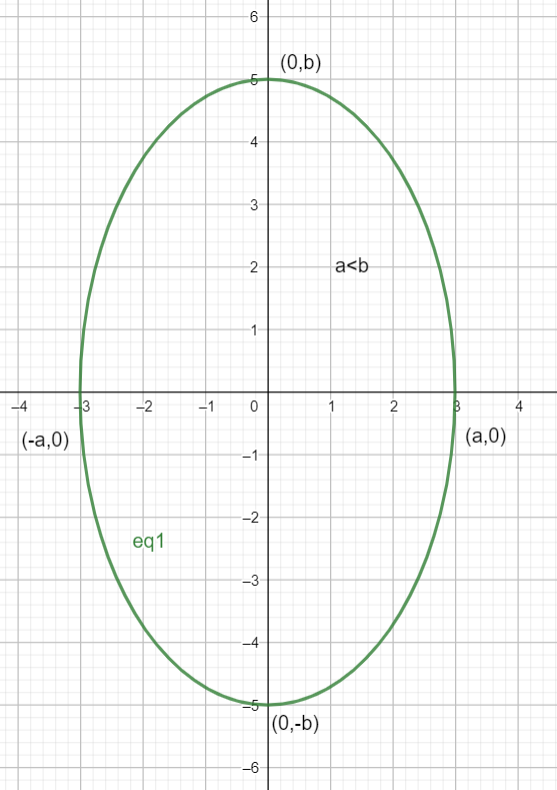
Comparing the equation given in the question, to the general formula of an ellipse, we get that :
${{a}^{2}}=f({{k}^{2}}+2k+5)$ and ${{b}^{2}}=f(k+11)$
It is told that the major axis of this ellipse should coincide with the $x$ axis.
This means that the $x$ axis has the major axis of the ellipse, and for that to be possible, we need that $b < a$.
Therefore, for this ellipse we need that :
$\begin{aligned} & a > b \\\ & \Rightarrow \sqrt{f({{k}^{2}}+2k+5)} > \sqrt{f(k+11)} \\\ \end{aligned}$
Squaring both sides, we get :
$f({{k}^{2}}+2k+5) > f(k+11)$

Now, we’re given that $f(x)$ is a positive decreasing function. The fact that it is a decreasing function means that it gives a lower value of $f(x)$ at a higher value of $x$. Written mathematically, it means that :
If $\begin{aligned} & f({{x}_{1}}) > f({{x}_{2}}) \\\ & \Rightarrow {{x}_{1}} < {{x}_{2}} \\\ \end{aligned}$
Applying this result to the inequality we got from the ellipse, we can say that
$\begin{aligned} f({{k}^{2}}+2k+5) > f(k+11) \\\ \Rightarrow {{k}^{2}}+2k+5 < k+11 \\\ \Rightarrow {{k}^{2}}+k-6 < 0 \\\ \Rightarrow {{k}^{2}}+3k-2k-6 < 0 \\\ \Rightarrow k(k+3)-2(k+3) < 0 \\\ \Rightarrow (k-2)(k+3) < 0 \\\ \end{aligned}$
Now, we know that the sign of a product of two numbers will be negative when the signs of the individual numbers to be multiplied are opposite. Therefore, the last step will be satisfied when
(k-2) is positive and (k+3) is negative $\Rightarrow k-2 > 0\text{ and }k+3 < 0\Rightarrow k > 2\text{ and }k < -3$ which is never possible....................................(i)
Or
(k-2) is negative and (k+3) is positive $\Rightarrow k-2 < 0\text{ and }k+3 > 0\Rightarrow k < 2\text{ and }k > -3$ which means that k should lie in the interval $k\in (-3,2)$
Thus, for the given condition, the interval which $k$ belongs to should be (-3,2) which matches option (c). Therefore, option (c) is the correct answer.

Note: Some knowledge of increasing and decreasing functions is used in this question. So, you should revise the theory of that topic a bit, before attempting this question. In general, for an increasing function,
If $\begin{aligned} & f({{x}_{1}}) > f({{x}_{2}}) \\\ & \Rightarrow {{x}_{1}} > {{x}_{2}} \\\ \end{aligned}$
And for a decreasing function, if $\begin{aligned} & f({{x}_{1}}) > f({{x}_{2}}) \\\ & \Rightarrow {{x}_{1}} < {{x}_{2}} \\\ \end{aligned}$.