Question

Consider the differential equation, $\frac{dy}{dx}$ + P(x)y = Q(x). If u(x), v(x) and w(x) are particular solutions different from u(x) and v(x) then find the ratio $\frac{v(x) - u(x)}{w(x) - u(x)}$.

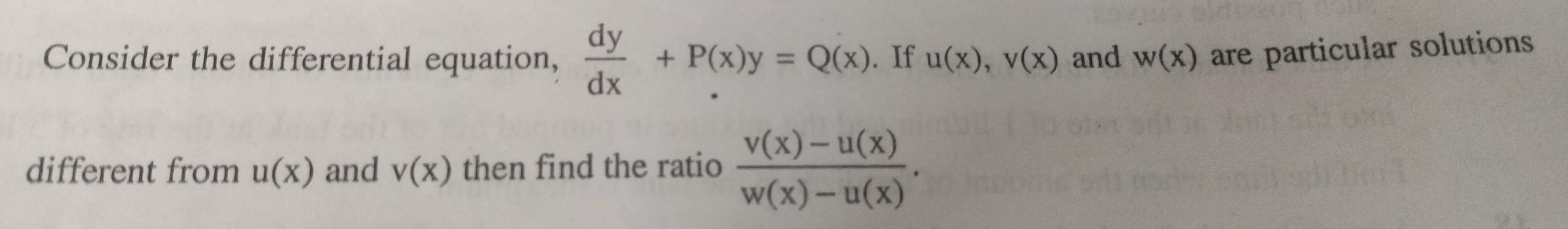
Answer 1

The ratio $\frac{v(x)-u(x)}{w(x)-u(x)}$ is a constant (specifically, $\frac{C_1}{C_2}$).

Answer 2

For the first order linear ODE

$$\frac{dy}{dx} + P(x)y = Q(x),$$

if $u(x)$ is a particular solution, the general solution is given by

$$y = u(x) + C e^{-\int P(x)\,dx}.$$

Thus, if

$$v(x) = u(x) + C_1 e^{-\int P(x)\,dx} \quad \text{and} \quad w(x) = u(x) + C_2 e^{-\int P(x)\,dx},$$

then

$$v(x) - u(x) = C_1 e^{-\int P(x)\,dx} \quad \text{and} \quad w(x) - u(x) = C_2 e^{-\int P(x)\,dx}.$$

The ratio is

$$\frac{v(x)-u(x)}{w(x)-u(x)} = \frac{C_1}{C_2},$$

which is independent of $x$; that is, it is a constant.