Question

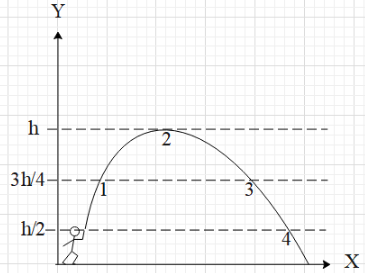
Consider the diagram of the trajectory of a thrown tomato. At what point is the potential energy greatest?

Answer 1

We need to find the point at which the potential energy will be maximum. There are five points given in the question. Calculate the potential energy at each point and then compare the potential energy. Accordingly, choose the point with the greatest potential energy.

Complete step by step answer:
We are given a projectile motion. In this question, a man has projected a tomato with some angle with the horizontal and the tomato is thrown with some initial velocity. We need to find the point which has the greatest energy. Potential energy or gravitational potential energy is the energy that a particle has by virtue of its position with respect to some zero potential reference point. As the object raises above this zero-potential surface, the magnitude of the potential energy increases. The formula to calculate magnitude of the potential energy, considering the X-axis to be at zero potential is
$PE = mgh$
Where $PE$ denotes the potential energy, $m$ is the mass of the object, $g$ is the acceleration due to gravity and $h$ denotes the height of the object above the zero-potential surface.

Let us now calculate the potential at each of five points;
The given heights are ${h_1} = \dfrac{3}{4}h$ , ${h_2} = h$ , ${h_3} = \dfrac{3}{4}h$ , ${h_4} = \dfrac{1}{2}h$ and ${h_1} = 0$ .
The magnitude of the potential energy for each point will be;
$\Rightarrow P{E_1} = mg\left( {\dfrac{3}{4}h} \right)$
$\Rightarrow P{E_2} = mg\left( h \right)$
$\Rightarrow P{E_3} = mg\left( {\dfrac{3}{4}h} \right)$
$\Rightarrow P{E_4} = mg\left( {\dfrac{1}{2}h} \right)$
$\therefore P{E_5} = mg\left( 0 \right) = 0$
The product $mg$ will be the same in each case, therefore the greatest value will be the one having greatest height. The height is maximum at point $2$ .

Therefore, the greatest potential energy is at point $2$.

Note: At point $2$ the kinetic energy is zero. The potential energy is minimum at point $5$ . The potential energy is maximum when the height of the object is maximum when the object is at maximum height with respect to the zero-potential surface. When the potential energy is minimum, the kinetic energy will be maximum.