Question

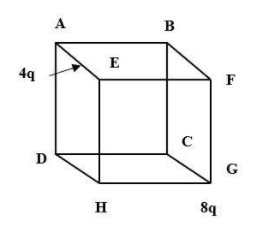
Consider the cube shown. A point charge 8q is placed at the vertex G of the cube and another charge 4q is placed at the center of an edge AE of the cube. Electric flux through the cube is

A. $\dfrac {q}{{\epsilon}_{0}}$
B. $\dfrac {2q}{{\epsilon}_{0}}$
C. $\dfrac {12q}{{\epsilon}_{0}}$
D. Zero

Answer 1

Consider cubes around the given cube and cubes above it. Then, find the flux passing through each cube due to charge 8q and 4q. Use Gauss's law to find the flux due to charge 4q and then charge 8q. Sum of fluxes due to both the charge will give the electric charge through the cube. Thus, add both the charges. The value obtained will be the electric charge through the cube.
Formula used:
$\phi = \dfrac {q}{{\epsilon}_{0}}$

Complete answer:
Consider three similar cubes placed at three sides of the cube and four cubes above these four cubes. So, the flux passing through each cube due to charge 8q will be $\dfrac {1}{8}$ of the flux. Similarly, flux due to charge 4q will be $\dfrac {1}{4}$ of the flux.
According to Gauss law, flux is given by,
$\phi = \dfrac {q}{{\epsilon}_{0}}$
Using the above equation, flux due to charge 4q is given by,
${\phi}_{1}=\dfrac {4q}{{\epsilon}_{0}}\times \dfrac {1}{4}$
$\therefore {\phi}_{1}=\dfrac {q}{{\epsilon}_{0}}$ …(1)
Similarly, flux due to charge 8q is given by,
${\phi}_{2}=\dfrac {8q}{{\epsilon}_{0}}\times \dfrac {1}{8}$
$\therefore {\phi}_{2}=\dfrac {q}{{\epsilon}_{0}}$ …(2)
Total flux through the cube is given by,
$\phi ={\phi}_{1} +{\phi}_{2}$
Substituting the values in above equation from equation. (2) and (3) we get,
$\phi =\dfrac {q}{{\epsilon}_{0}}+\dfrac {q}{{\epsilon}_{0}}$
$\therefore \phi =\dfrac {2q}{{\epsilon}_{0}}$
Thus, the electric flux through the cube is $\dfrac {2q}{{\epsilon}_{0}}.$

Hence, the correct answer is option B i.e. $\dfrac {2q}{{\epsilon}_{0}}.$

Note:
Electric field is just the measure of the distribution of electric field through an area. It is used to tell how much electric field strength is present at any distance from the charge which is responsible for the field. Unit of electric flux is Newton-meters squared per Coulomb $(N {m}^{2}{C}^{-1})$ or Volt meters $(Vm)$. Electric flux does not depend on the direction. Hence, it is a scalar quantity.