Question

Consider the cube in the first octant with sides OP, OQ and OR of length 1, along the x axis, y axis and z axis respectively, where O(0,0,0) is the origin. Let $S=\left( \dfrac{1}{2},\dfrac{1}{2},\dfrac{1}{2} \right)$ be the center of the cube and T be the vertex of the cube opposite to the origin O such that S lies on the diagonal OT. If $\vec{p}=\overrightarrow{SP},\vec{q}=\overrightarrow{SQ},\vec{r}=\overrightarrow{SR}\text{ and }\vec{t}=\overrightarrow{ST}$, then the value of $2\left| \left( \vec{p}\times \vec{q} \right)\times \left( \vec{r}\times \vec{t} \right) \right|$ is:

Answer 1

In this question, we are given a cube along with its coordinates are some other information. We have to find $2\left| \left( \vec{p}\times \vec{q} \right)\times \left( \vec{r}\times \vec{t} \right) \right|$ where $\vec{p}=\overrightarrow{SP},\vec{q}=\overrightarrow{SQ},\vec{r}=\overrightarrow{SR}\text{ and }\vec{t}=\overrightarrow{ST}$. For this, we will first draw diagram to understand question and find coordinate of P, Q R, S and T. Using them, we will evaluate $\vec{p},\vec{q},\vec{r}\text{ and }\vec{t}$. $\overrightarrow{AB}$ is given by $\left( \text{positive vector of }\vec{B} \right)-\left( \text{positive vector of }\vec{A} \right)$. After that, we will evaluate $2\left| \left( \vec{p}\times \vec{q} \right)\times \left( \vec{r}\times \vec{t} \right) \right|$ for two vector $\vec{a}={{a}_{1}}\hat{i}+{{a}_{2}}\hat{j}+{{a}_{3}}\hat{k}\text{ and }\vec{b}={{b}_{1}}\hat{i}+{{b}_{2}}\hat{j}+{{b}_{3}}\hat{k}$.
$\vec{a}\times \vec{b}$ is given by $\vec{a}\times \vec{b}\left| \begin{matrix} {\hat{i}} & {\hat{j}} & {\hat{k}} \\\ {{a}_{1}} & {{a}_{2}} & {{a}_{3}} \\\ {{b}_{1}} & {{b}_{2}} & {{b}_{3}} \\\ \end{matrix} \right|$.

Complete step-by-step solution
Let us draw a diagram with the given information:

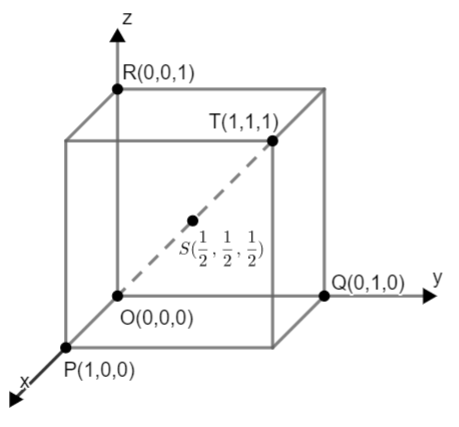
Here OP, OQ, and OR are given as of length 1, therefore coordinates of OP, OQ, and OR become (1,0,0), (0,1,0), and (0,0,1) respectively.
Coordinates of S are given as $\left( \dfrac{1}{2},\dfrac{1}{2},\dfrac{1}{2} \right)$ and since T is the opposite corner of cube from origin, so its distance from x axis, y axis and z axis will be 1. So, coordinates of T are (1,1,1). Therefore, coordinates are:

& Q=\left( 0,1,0 \right) \\\ & S=\left( \dfrac{1}{2},\dfrac{1}{2},\dfrac{1}{2} \right) \\\ & T=\left( 1,1,1 \right) \\\ & P=\left( 1,0,0 \right) \\\ & R=\left( 0,0,1 \right) \\\ \end{aligned}$$ Position vector becomes: $$\begin{aligned} & \overrightarrow{Q}=\hat{j} \\\ & \overrightarrow{S}=\dfrac{1}{2}\hat{i}+\dfrac{1}{2}\hat{j}+\dfrac{1}{2}\hat{k} \\\ & \overrightarrow{T}=\hat{i}+\hat{j}+\hat{k} \\\ & \overrightarrow{P}=\hat{i} \\\ & R=\hat{k} \\\ \end{aligned}$$ Now, let us find $\vec{p},\vec{q},\vec{r}\text{ and }\vec{t}$. $$\begin{aligned} & \vec{p}=\overrightarrow{SP}=\left( \text{positive vector of }\vec{P} \right)-\left( \text{positive vector of }\vec{S} \right) \\\ & \Rightarrow \left( {\hat{i}} \right)-\left( \dfrac{1}{2}\hat{i}+\dfrac{1}{2}\hat{j}+\dfrac{1}{2}\hat{k} \right) \\\ & \Rightarrow \dfrac{1}{2}\hat{i}-\dfrac{1}{2}\hat{j}-\dfrac{1}{2}\hat{k} \\\ & \Rightarrow \dfrac{1}{2}\left( \hat{i}-\hat{j}-\hat{k} \right) \\\ \end{aligned}$$ $$\begin{aligned} & \vec{q}=\overrightarrow{SQ}=\left( \text{positive vector of }\overrightarrow{Q} \right)-\left( \text{positive vector of }\vec{S} \right) \\\ & \Rightarrow \left( {\hat{j}} \right)-\left( \dfrac{1}{2}\hat{i}+\dfrac{1}{2}\hat{j}+\dfrac{1}{2}\hat{k} \right) \\\ & \Rightarrow -\dfrac{1}{2}\hat{i}+\dfrac{1}{2}\hat{j}-\dfrac{1}{2}\hat{k} \\\ & \Rightarrow \dfrac{1}{2}\left( -\hat{i}+\hat{j}-\hat{k} \right) \\\ \end{aligned}$$ $$\begin{aligned} & \vec{r}=\overrightarrow{SR}=\left( \text{positive vector of }\overrightarrow{R} \right)-\left( \text{positive vector of }\vec{S} \right) \\\ & \Rightarrow \left( {\hat{k}} \right)-\left( \dfrac{1}{2}\hat{i}+\dfrac{1}{2}\hat{j}+\dfrac{1}{2}\hat{k} \right) \\\ & \Rightarrow -\dfrac{1}{2}\hat{i}-\dfrac{1}{2}\hat{j}+\dfrac{1}{2}\hat{k} \\\ & \Rightarrow \dfrac{1}{2}\left( -\hat{i}-\hat{j}+\hat{k} \right) \\\ \end{aligned}$$ $$\begin{aligned} & \vec{t}=\overrightarrow{ST}=\left( \text{positive vector of }\vec{T} \right)-\left( \text{positive vector of }\vec{S} \right) \\\ & \Rightarrow \left( \hat{i}+\hat{j}+\hat{k} \right)-\left( \dfrac{1}{2}\hat{i}+\dfrac{1}{2}\hat{j}+\dfrac{1}{2}\hat{k} \right) \\\ & \Rightarrow \dfrac{1}{2}\hat{i}+\dfrac{1}{2}\hat{j}+\dfrac{1}{2}\hat{k} \\\ & \Rightarrow \dfrac{1}{2}\left( \hat{i}+\hat{j}+\hat{k} \right) \\\ \end{aligned}$$ Now let us calculate $\vec{p}\times \vec{q}$ we get: $\vec{p}\times \vec{q}=\dfrac{1}{4}\left( \hat{i}-\hat{j}-\hat{k} \right)\times \left( -\hat{i}+\hat{j}-\hat{k} \right)$. $\vec{p}\times \vec{q}$ becomes equal to $\dfrac{1}{4}\left| \begin{matrix} {\hat{i}} & {\hat{j}} & {\hat{k}} \\\ 1 & -1 & -1 \\\ -1 & 1 & -1 \\\ \end{matrix} \right|$. $$\begin{aligned} & \Rightarrow \dfrac{1}{4}\left( \hat{i}\left( 1+1 \right)-\hat{j}\left( -1-1 \right)+\hat{k}\left( 1-1 \right) \right) \\\ & \Rightarrow \dfrac{1}{4}\left( 2\hat{i}+2\hat{j} \right) \\\ & \Rightarrow \dfrac{1}{2}\left( \hat{i}+\hat{j} \right) \\\ \end{aligned}$$ Therefore, we get $\vec{p}\times \vec{q}$ to be equal to $\dfrac{1}{2}\left( \hat{i}+\hat{j} \right)$. Now, let us calculate $\vec{r}\times \vec{t}$ we get: $\vec{r}\times \vec{t}=\dfrac{1}{4}\left( -\hat{i}-\hat{j}+\hat{k} \right)\times \left( \hat{i}+\hat{j}+\hat{k} \right)$. $\vec{r}\times \vec{t}$ becomes equal to $\dfrac{1}{4}\left| \begin{matrix} {\hat{i}} & {\hat{j}} & {\hat{k}} \\\ -1 & -1 & 1 \\\ 1 & 1 & 1 \\\ \end{matrix} \right|$. $$\begin{aligned} & \Rightarrow \dfrac{1}{4}\left( \hat{i}\left( -1-1 \right)-\hat{j}\left( -1-1 \right)+\hat{k}\left( -1+1 \right) \right) \\\ & \Rightarrow \dfrac{1}{4}\left( -2\hat{i}+2\hat{j} \right) \\\ & \Rightarrow \dfrac{1}{2}\left( -\hat{i}+\hat{j} \right) \\\ \end{aligned}$$ Therefore, we get $\vec{r}\times \vec{t}$ to be equal to $\dfrac{1}{2}\left( -\hat{i}+\hat{j} \right)$. Now we need to calculate $\left( \vec{p}\times \vec{q} \right)\times \left( \vec{r}\times \vec{t} \right)$ therefore, $\left( \vec{p}\times \vec{q} \right)\times \left( \vec{r}\times \vec{t} \right)=\dfrac{1}{4}\left( \hat{i}+\hat{j} \right)\times \left( -\hat{i}+\hat{j} \right)$. $$\begin{aligned} & \left( \vec{p}\times \vec{q} \right)\times \left( \vec{r}\times \vec{t} \right)=\dfrac{1}{4}\left| \begin{matrix} {\hat{i}} & {\hat{j}} & {\hat{k}} \\\ 1 & 1 & 0 \\\ -1 & 1 & 0 \\\ \end{matrix} \right| \\\ & \Rightarrow \dfrac{1}{4}\left( \hat{k}\left( 1+1 \right) \right) \\\ & \Rightarrow \dfrac{1}{2}\hat{k} \\\ \end{aligned}$$ Now magnitude of $\left( \vec{p}\times \vec{q} \right)\times \left( \vec{r}\times \vec{t} \right)$ will be given by $\left| \left( \vec{p}\times \vec{q} \right)\times \left( \vec{r}\times \vec{t} \right) \right|=\dfrac{1}{2}\left| {\hat{k}} \right|$. As we know, $\hat{i},\hat{j},\hat{k}$ are unit vectors, so $\left| {\hat{k}} \right|$ will be equal to 1. Therefore, $\left| \left( \vec{p}\times \vec{q} \right)\times \left( \vec{r}\times \vec{t} \right) \right|=\dfrac{1}{2}\left( 1 \right)=\dfrac{1}{2}$. Multiplying both sides by 2, we get: $2\left| \left( \vec{p}\times \vec{q} \right)\times \left( \vec{r}\times \vec{t} \right) \right|=2\times \dfrac{1}{2}=1$. Hence 1 is our required answer. **Note:** Students should always draw diagrams for understanding these questions better. Take care of signs while calculating determinants. While calculating $\overrightarrow{SP}$ make sure that the position vector of $\vec{S}$ is subtracted from the position vector of $\vec{P}$ and not vice versa. Students should note that, magnitude of $\hat{i},\hat{j},\hat{k}$ is always 1.