Question

Consider the circuit shown in figure. Suppose the switch which has been connected to point A for a long time is suddenly thrown to B at t = 0, then

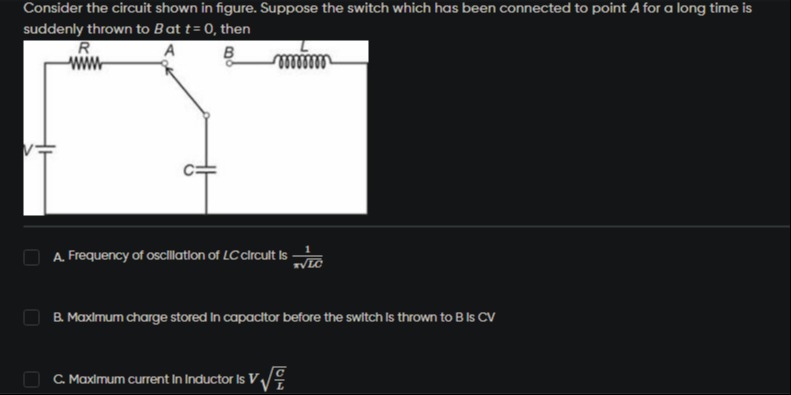
• A. Frequency of oscillation of LC circuit is $\frac{1}{\pi \sqrt{LC}}$
• B. Maximum charge stored in capacitor before the switch is thrown to B is CV
• C. Maximum current in Inductor is $V\sqrt{\frac{C}{L}}$

Answer 1

Answer: (B), (C)

B, C

Answer 2

When the switch is connected to point A for a long time, the capacitor C is fully charged to the voltage of the source V, so the initial charge on the capacitor is $Q_0 = CV$.

At t=0, the switch is thrown to point B, connecting the charged capacitor to the inductor L, forming an LC circuit. The initial conditions for the oscillation are $q(0) = CV$ and $i(0) = 0$.

The angular frequency of oscillation in an ideal LC circuit is $\omega = \frac{1}{\sqrt{LC}}$. The frequency of oscillation is $f = \frac{\omega}{2\pi} = \frac{1}{2\pi \sqrt{LC}}$. Option A is incorrect as it states the frequency is $\frac{1}{\pi \sqrt{LC}}$.

The maximum charge stored in the capacitor during the oscillation is equal to the initial charge, $Q_{max} = CV$. Option B is correct.

The total energy in the LC circuit is conserved. Initially, the energy is stored in the capacitor: $U_{initial} = \frac{1}{2}CV^2$. When the current in the inductor is maximum ($I_{max}$), the charge on the capacitor is zero, and all the energy is stored in the inductor: $U_{max\_inductor} = \frac{1}{2}LI_{max}^2$. Equating the energies: $\frac{1}{2}CV^2 = \frac{1}{2}LI_{max}^2$ $I_{max}^2 = \frac{CV^2}{L}$ $I_{max} = V\sqrt{\frac{C}{L}}$ Option C is correct.