Question

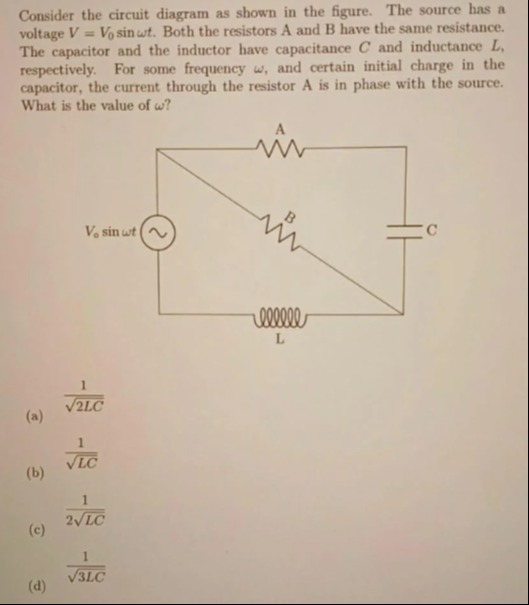
Consider the circuit diagram as shown in the figure. The source has a voltage $V = V_0 \sin \omega t$. Both the resistors A and B have the same resistance. The capacitor and the inductor have capacitance $C$ and inductance $L$, respectively. For some frequency $\omega$, and certain initial charge in the capacitor, the current through the resistor A is in phase with the source. What is the value of $\omega$?

• A. $\frac{1}{\sqrt{2LC}}$
• B. $\frac{1}{\sqrt{LC}}$
• C. $\frac{1}{2\sqrt{LC}}$
• D. $\frac{1}{\sqrt{3LC}}$

Answer 1

Answer: (A)

$\omega = \frac{1}{\sqrt{2LC}}$

Answer 2

To find the frequency $\omega$ at which the current through resistor A is in phase with the source voltage, we need to analyze the circuit's impedance. The key is to ensure that the imaginary part of the total admittance of the parallel branches (capacitor and resistor-inductor series) is zero. This condition makes the overall impedance purely real, leading to the current being in phase with the voltage.

Here's a breakdown of the solution:

1. Calculate Impedances:

   • Impedance of the capacitor branch: $Z_1 = \frac{1}{j\omega C}$
   • Impedance of the resistor-inductor branch: $Z_2 = R + j\omega L$

2. Calculate Admittances:

   • Admittance of the capacitor branch: $Y_1 = j\omega C$
   • Admittance of the resistor-inductor branch: $Y_2 = \frac{1}{R + j\omega L} = \frac{R - j\omega L}{R^2 + \omega^2 L^2}$

3. Total Admittance: The total admittance of the parallel branches is the sum of individual admittances:

   $$Y_{total} = Y_1 + Y_2 = j\omega C + \frac{R - j\omega L}{R^2 + \omega^2 L^2} = \frac{R}{R^2 + \omega^2 L^2} + j\left(\omega C - \frac{\omega L}{R^2 + \omega^2 L^2}\right)$$

4. In-Phase Condition: For the current to be in phase with the voltage, the imaginary part of the total admittance must be zero:

   $$\omega C - \frac{\omega L}{R^2 + \omega^2 L^2} = 0$$

5. Solve for $\omega$:

   $$\omega C = \frac{\omega L}{R^2 + \omega^2 L^2}$$ $$C = \frac{L}{R^2 + \omega^2 L^2}$$ $$R^2 + \omega^2 L^2 = \frac{L}{C}$$

6. Choose R for Frequency Independence: To make the frequency independent of the resistance $R$, we choose $R^2 = \frac{L}{2C}$. Substituting this into the equation:

   $$\frac{L}{2C} + \omega^2 L^2 = \frac{L}{C}$$ $$\omega^2 L^2 = \frac{L}{C} - \frac{L}{2C} = \frac{L}{2C}$$ $$\omega^2 = \frac{1}{2LC}$$ $$\omega = \frac{1}{\sqrt{2LC}}$$

Therefore, the value of $\omega$ for which the current through resistor A is in phase with the source is $\frac{1}{\sqrt{2LC}}$.