Question
Question: Consider the circuit below where all resistors are of \(1k\Omega \). If a current of magnitude 1mA f...
Consider the circuit below where all resistors are of 1kΩ. If a current of magnitude 1mA flows through the resistor marked X. What is the potential difference measured between points P and Q:-
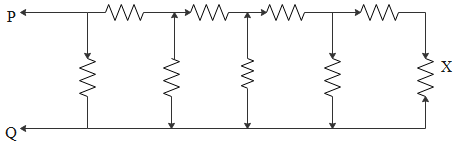
(1) 21V
(2) 68V
(3) 55V
(4) 34V
Solution
To calculate the potential difference between two points P and Q first we have to draw the equivalent circuit of the given circuit. Given that all the resistance are equal and are equal to R. Then calculate the current across each resistor and then by substituting the given value of current and resistor we will get the potential difference between P and Q.
Complete step-by-step solution:
Given that,
R=1kΩ
i=1mA=1×10−3A
The given circuit is,
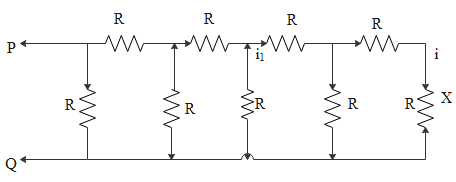
To calculate ‘i’ we should first consider the three resistors at the right hand side and thus the equivalent resistance will be 3R. Then analyse the current across the other branch.
Then the value of i can be calculated as,
i=3Ri1×R=3i1
∴i1=3i
When the three resistors in the right side of the circuit is replaced by the equivalent circuit the circuit becomes,
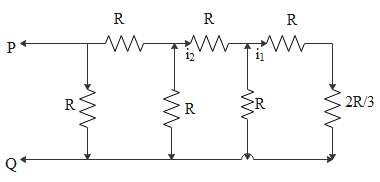
That is, in the above circuit the two resistors at the right side is in series and the third one is parallel to these two resistors. Thus here the three resistors are replaced by an equivalent resistor of 32R.
Then calculate the current i1. That is,
i1=i2×83
i2=38i1
⇒i2=38×3i∴i2=8i
Similarly again replace the resistors at the end by an equivalent resistor. Thus the circuit becomes,
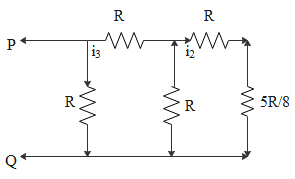
i2=i3×218
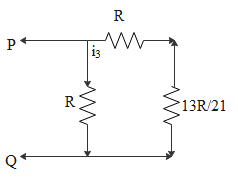
i3=821i2=821×8i=21i
Then the potential difference,
VP−VQ=i3×[R+2113R]
=i3×2134R
Substituting the value of i3equation becomes,
VP−VQ=21i×[2134R]
=34iR
Given the value of i and R. That is,
i=1mA=1×10−3A
R=1kΩ
Thus,
VP−VQ=34×1×10−3×1×103
=34volt
Therefore option (D) is correct.
Note: The potential difference between any two points can be otherwise called the voltage. And if the distance between these two points is infinite, then the resultant potential difference or voltage is equal to zero. The SI unit of potential difference is volts.
