Question

Consider the charges q, q and –q placed at the vertices of the equilateral triangle, as shown in the figure. What is the force on each charge?

Answer 1

Emissive power is the radiant energy emitted by the Body. Body should be anything either it is black or gray, coefficient of emission is the fractional part of power of a perfectly black Body at the same temperature.

Formula Used: - $F=k\dfrac{{{q}_{1}}{{q}_{2}}}{{{d}^{2}}}$
Where,
K is the Coulomb’s constant
${{q}_{1}}{{q}_{2}}$ are the charges
${{d}^{2}}$ is the distance between the two charge

Complete step by step answer:
The electric force between two static and charged particles is called an electrostatic force. The nature of this force can be attractive or repulsive depending on whether the particles are positively/negatively charged. Coulomb’s law provides us the equation which relates the force and the charged particles along with the distance in the given charged particles.
In this question the length of the equilateral triangle is not given. Therefore, we will assume it to be l.
Now from Coulomb’s law
We know,
$F=k\dfrac{{{q}_{1}}{{q}_{2}}}{{{d}^{2}}}$
Now, let us calculate the force on first particle 1 say ${{F}_{1}}$ with charge q as shown in the figure below.

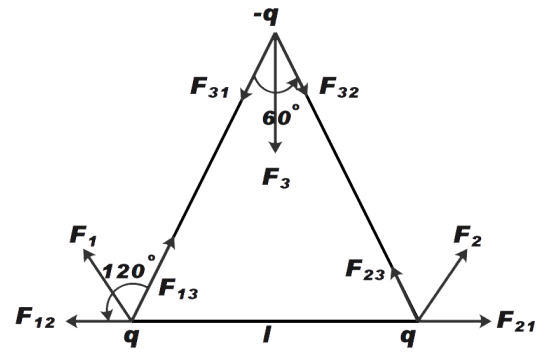
Now, we know that particles with the same charge repel each other and that with opposite charges attract each other. Therefore, as shown in figure ${{F}_{1}}$ is the resultant of repulsive force on particle 1 by 2 say force ${{F}_{12}}$ and attractive force by 3 on 1 say force ${{F}_{13}}$
Now for, the charge on both particles is equal in magnitude as well as direction and distance is taken as l
Therefore, Coulomb’s law can be modified as
${{F}_{12}}=k\dfrac{{{q}_{1}}{{q}_{2}}}{{{d}^{2}}}$
After substituting the values
We get,
${{F}_{12}}=k\dfrac{{{q}^{2}}}{{{l}^{2}}}$
Let,
$k\dfrac{{{q}^{2}}}{{{l}^{2}}}=F$…………………………….. (1)
Therefore,
$\left| {{F}_{12}} \right|=F$ ……………….. (2)
Similarly, for force ${{F}_{13}}$
${{F}_{13}}=k\dfrac{{{q}_{1}}{{q}_{2}}}{{{d}^{2}}}$
After substituting values,
We get,
${{F}_{13}}=\left( -k\dfrac{{{q}^{2}}}{{{l}^{2}}} \right)$ ……………. (since charge on particle 3 is negative)
$\left| {{F}_{13}} \right|=F$ ……………… (3)
Similarly, if we calculate the magnitude of other forces say ${{F}_{21}},{{F}_{23}},{{F}_{31}},{{F}_{32}}$
We will get the same result
Therefore,
$\left| {{F}_{21}} \right|=\left| {{F}_{23}} \right|=\left| {{F}_{31}} \right|=\left| {{F}_{32}} \right|=F$ ………………. (4)
Now we know that ${{F}_{1}}$ is the resultant of ${{F}_{12}}$ and ${{F}_{13}}$. Also, the angle between the two forces is 120 degrees.
Therefore, from (2) and (3)
We get,
${{F}_{1}}=\sqrt{{{F}^{2}}+{{F}^{2}}+2\times F\times F\cos 120}$
On solving
We get,
${{F}_{1}}=F$ …………… (since $\cos 120=-\dfrac{1}{2}$) ……………….. (A)
Now, since the distance between the charge 1 and 2 is the same, also their charge and other factors such as angle and magnitude of component forces is the same. From the figure, we can say that
${{F}_{1}}={{F}_{2}}$
Therefore,
${{F}_{2}}=F$ ……………………………………. (B)
Now, for charge 3, we can say that angle between the component vector force say ${{F}_{31}}$and ${{F}_{32}}$ of force${{F}_{3}}$ is 60 degrees .
Therefore, the magnitude resultant force ${{F}_{3}}$ after substituting values of ${{F}_{31}}$and ${{F}_{32}}$ will be given by,
${{F}_{3}}=\sqrt{{{F}^{2}}+{{F}^{2}}+2\times F\times F\cos 60}$
On solving
We get,
${{F}_{3}}=\sqrt{3}F$………………… (since $cos60\text{ }=\dfrac{1}{2}$) …………… (C)
Now, from (1) we know that
$k\dfrac{{{q}^{2}}}{{{l}^{2}}}=F$
Therefore, from (1), (A) and (B)
We get,
${{F}_{2}}={{F}_{2}}=k\dfrac{{{q}^{2}}}{{{l}^{2}}}$
Also from (1) and (C
We get,
${{F}_{3}}=\sqrt{3}k\dfrac{{{q}^{2}}}{{{l}^{2}}}$
Therefore, force on charged particle q, q and –q is $k\dfrac{{{q}^{2}}}{{{l}^{2}}}$, $k\dfrac{{{q}^{2}}}{{{l}^{2}}}$, $\sqrt{3}k\dfrac{{{q}^{2}}}{{{l}^{2}}}$ respectively.

Note:
The Coulomb’s constant k is given as,
$k=\dfrac{1}{4\pi {{\varepsilon }_{o}}}$
Where, ${{\varepsilon }_{o}}$is the vacuum electric permittivity. The value of k is generally taken as $k=8.9875\times {{10}^{9}}N.{{m}^{2}}/{{C}^{2}}$