Question

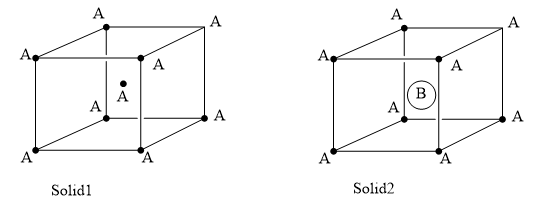
Consider the bcc unit cells of the solids 1 and 2 with the position of atoms as shown below. The radius of atom B is twice that of atom A. The unit cell edge length is $50$ more in solid 2 than in 1. What is the approximate packing efficiency in solid 2?

(A)- $45$
(B)- $65$
(C)- $90$
(D)- $75$

Answer 1

The packing efficiency accounts for the fraction of the unit cell occupied by the atoms, by taking the percent of the volume of the total atoms to the volume of the cube.

Complete step by step answer:
It is given that both the solids are body-centred cubic unit cells, that is, there are eight atoms at the corner of the cell and one whole atom in the centre of the unit cell. Each corner atom in the cell is shared among eight other adjacent unit cells. So, the contribution of a single corner atom is ${{(1/8)}^{th}}$ in the unit cell. Therefore, having a total eight corner atoms, the total contribution is $8\times \dfrac{1}{8}=$ 1 atom. In solid 2, there are eight corner A atoms, and one whole B atom at the centre of the unit cell. The total contribution from the eight corner A atoms is 1 atom and the contribution from the B atom is one. So, two total atoms are present in the unit cell. Then, the packing efficiency, that is the fraction of the unit cell occupied by the atoms is $=\dfrac{\text{volume of the 2 atoms}}{\text{total volume of the unit cell}}\times 100$ ----------- (a)
-Let the radius of atom A be ${{r}_{A}}=r$, then given that radius of atom B is twice that of A, so ${{r}_{B}}=2r$. ------------ (b)
-Then, the volume of atom A is $=\dfrac{4}{3}\pi r_{A}^{3}=\dfrac{4}{3}\pi {{r}^{3}}$
And volume of atom B is = $=\dfrac{4}{3}\pi r_{B}^{3}=\dfrac{4}{3}\pi {{(2r)}^{3}}$ --------- (c)
-Also, in the bcc unit cell, the relation of the length of body diagonal to the side of the cube is given by: $4r=\sqrt{3}a$ , where r is the radius and a is the length of side of the cube.
-Given, the length of the side of solid 2, ${{a}_{2}}$ is $50$ more than ${{a}_{1}}$ of solid 1. So, we have, ${{a}_{2}}={{a}_{1}}+\dfrac{50}{100}{{a}_{1}}=\dfrac{150}{100}{{a}_{1}}=\dfrac{3}{2}{{a}_{1}}$
From solid 1, we have the relation $4{{r}_{A}}=\sqrt{3}{{a}_{1}}$ or ${{a}_{1}}=\dfrac{4}{\sqrt{3}}{{r}_{A}}$ -------- (d)
Substituting the value of ${{a}_{1}}$ in ${{a}_{2}}$, we have ${{a}_{2}}=\dfrac{3}{2}\times \dfrac{4}{\sqrt{3}}{{r}_{A}}=2\sqrt{3}\,r$
-Then volume of the unit cell is ${{a}^{3}}={{({{a}_{2}})}^{3}}={{(2\sqrt{3}\,r)}^{3}}$ ---------- (e)
-Substituting the value of (c) and (e) in equation (a), we get,
Packing efficiency $=\dfrac{\text{volume of atom}\,\text{A}\,\text{+}\,\text{volume}\,\text{of}\,\text{atom}\,\text{B}}{\text{total volume of solid 2}}\times 100$
$=\dfrac{\dfrac{4}{3}\pi {{r}^{3}}+\dfrac{4}{3}\pi {{(2r)}^{3}}}{{{(2\sqrt{3}r)}^{3}}}\times 100\,\,$
$=\dfrac{\dfrac{4}{3}\pi {{r}^{3}}(1+8)}{8\times 3\sqrt{3}{{r}^{3}}}\times 100=\dfrac{\pi }{2\sqrt{3}}\times 100=90.6$

Therefore, the approximate packing efficiency in solid 2 is option (C)- $90$

Note: The atoms are taken to be spheres to account for its contribution in the unit cell, so the volume of the sphere is considered. There are a total two atoms in a body-centred cubic unit cell.