Question
Question: Consider the arrangement of three plates X, Y and Z each of the area A and separation d. The energy ...
Consider the arrangement of three plates X, Y and Z each of the area A and separation d. The energy stored when the plates are fully charged is: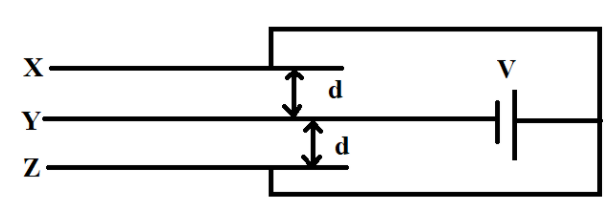
A) ε0A2dV2
B) ε0AdV2
C) 2ε0AdV2
D) 3ε0AdV2
Solution
Work has to be done to store energy in the plates. This work is converted into electrostatic potential energy and stored in the plates of the capacitor. To find the energy stored in the plates, we have to consider the plates as the plates of a capacitor and use the formula for the energy stored in the plates of a capacitor.
Formula used:
i) C=dAε0 (Where C stands for the capacitance of the capacitor, A stands for the area of the plates, ε0stands for the dielectric constant of free space, d stands for the distance between two plates)
ii) U=21CV2 (Where U stands for the energy stored in the capacitor, V stands for the potential difference)
Complete step by step solution:
In the diagram, the three plates can be considered as two capacitors.
Hence the capacitance is,
Cnet=C+C=2C
We know that the capacitance of a parallel plate capacitor is C=dε0A
Since the net capacitance is given by 2C, we can write
Cnet=d2ε0A
Now we have to find the energy stored in the plates by using the formula, U=21CV2
Here, U=21CnetV2
Substituting the value of Cnetin the equation
U=21(d2ε0A)V2
U=dε0AV2
The correct answer is option(B), ε0AdV2.
Note: Capacitors store electrical energy in an electrical field. According to the law of conservation of energy, the work done in storing the energy is converted into energy. To find the energy stored in the plates of a capacitor, two more formulae can be used.
If the charge Q and the capacitance C is given in the question we can use the equation, U=2CQ2.
If the charge Q and potential difference V is given, then use the equation, U=21QV.
