Question

Consider the AC circuit shown in the figure. Choose the correct option(s).

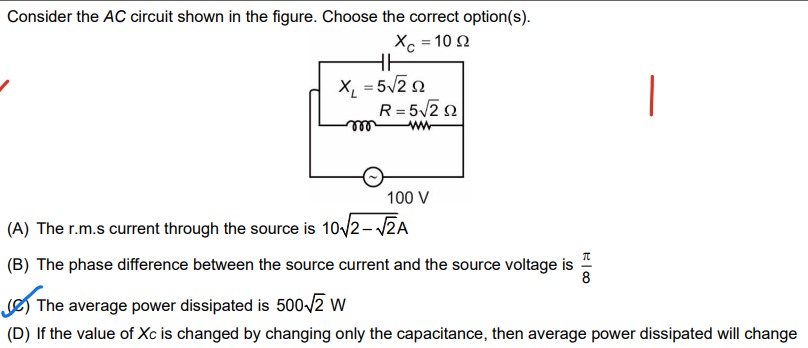
• A. The r.m.s current through the source is $10\sqrt{2}-\sqrt{2}A$
• B. The phase difference between the source current and the source voltage is $\frac{\pi}{8}$
• C. The average power dissipated is $500\sqrt{2}$ W
• D. If the value of $Xc$ is changed by changing only the capacitance, then average power dissipated will change

Answer 1

Answer: (B), (C)

B, C

Answer 2

The given AC circuit consists of a voltage source in parallel with a capacitor and a series combination of an inductor and a resistor. The rms voltage of the source is $V_{rms} = 100$ V. The capacitive reactance is $X_C = 10 \, \Omega$, the inductive reactance is $X_L = 5\sqrt{2} \, \Omega$, and the resistance is $R = 5\sqrt{2} \, \Omega$.

The voltage across each parallel branch is equal to the source voltage. The rms current through the capacitor is $I_{C,rms} = \frac{V_{rms}}{X_C} = \frac{100}{10} = 10$ A. This current leads the voltage by $90^\circ$. The impedance of the series RL branch is $Z_{RL} = R + jX_L = 5\sqrt{2} + j5\sqrt{2} \, \Omega$. The magnitude of the impedance is $|Z_{RL}| = \sqrt{R^2 + X_L^2} = \sqrt{(5\sqrt{2})^2 + (5\sqrt{2})^2} = \sqrt{50 + 50} = \sqrt{100} = 10 \, \Omega$. The rms current through the RL branch is $I_{RL,rms} = \frac{V_{rms}}{|Z_{RL}|} = \frac{100}{10} = 10$ A. The phase angle of the RL branch impedance is $\phi_{RL} = \arctan\left(\frac{X_L}{R}\right) = \arctan\left(\frac{5\sqrt{2}}{5\sqrt{2}}\right) = \arctan(1) = 45^\circ = \frac{\pi}{4}$ radians. The current through the RL branch lags the voltage by $\frac{\pi}{4}$.

To find the total rms current through the source, we need to add the currents from the two branches as phasors. Let the voltage be represented by a phasor $V = 100 \angle 0^\circ$. The current through the capacitor is $I_C = 10 \angle 90^\circ = 10j$. The current through the RL branch is $I_{RL} = 10 \angle -45^\circ = 10(\cos(-45^\circ) + j\sin(-45^\circ)) = 10\left(\frac{1}{\sqrt{2}} - j\frac{1}{\sqrt{2}}\right) = 5\sqrt{2} - j5\sqrt{2}$. The total source current is $I_{source} = I_C + I_{RL} = 10j + (5\sqrt{2} - j5\sqrt{2}) = 5\sqrt{2} + j(10 - 5\sqrt{2})$. The rms value of the source current is $|I_{source,rms}| = \sqrt{(5\sqrt{2})^2 + (10 - 5\sqrt{2})^2} = \sqrt{50 + 100 - 100\sqrt{2} + 50} = \sqrt{200 - 100\sqrt{2}} = 10\sqrt{2 - \sqrt{2}}$. Option (A) states the rms current is $10\sqrt{2}-\sqrt{2} = 9\sqrt{2}$. Since $10\sqrt{2 - \sqrt{2}} \neq 9\sqrt{2}$, option (A) is incorrect.

The phase angle of the source current relative to the voltage is $\phi_{source} = \arctan\left(\frac{10 - 5\sqrt{2}}{5\sqrt{2}}\right) = \arctan\left(\frac{10}{5\sqrt{2}} - \frac{5\sqrt{2}}{5\sqrt{2}}\right) = \arctan\left(\frac{2}{\sqrt{2}} - 1\right) = \arctan(\sqrt{2} - 1)$. We know that $\tan(\frac{\pi}{8}) = \sqrt{2} - 1$. Since the real and imaginary parts of $I_{source}$ are positive, the phase angle is $\frac{\pi}{8}$. The phase difference between the source current and the source voltage is $|\phi_{source}| = \frac{\pi}{8}$. Option (B) states that the phase difference is $\frac{\pi}{8}$. This is correct.

The average power dissipated in the circuit is dissipated only in the resistor. The capacitor and inductor do not dissipate average power. The average power dissipated in the resistor is $P_{avg} = I_{RL,rms}^2 R$. We found $I_{RL,rms} = 10$ A and $R = 5\sqrt{2} \, \Omega$. $P_{avg} = (10)^2 \times 5\sqrt{2} = 100 \times 5\sqrt{2} = 500\sqrt{2}$ W. Option (C) states that the average power dissipated is $500\sqrt{2}$ W. This is correct.

If the value of $X_C$ is changed by changing only the capacitance, the impedance of the capacitor branch changes. However, the voltage across the RL branch remains the source voltage, and the impedance of the RL branch ($Z_{RL} = R + jX_L$) remains unchanged since $R$ and $X_L$ are not changed. The rms current through the RL branch is $I_{RL,rms} = \frac{V_{rms}}{|Z_{RL}|}$. Since $V_{rms}$ and $|Z_{RL}|$ are unchanged, $I_{RL,rms}$ remains unchanged. The average power dissipated is $P_{avg} = I_{RL,rms}^2 R$. Since $I_{RL,rms}$ and $R$ are unchanged, the average power dissipated remains unchanged. Option (D) states that if the value of $X_C$ is changed by changing only the capacitance, then average power dissipated will change. This is incorrect.

The correct options are (B) and (C).