Question

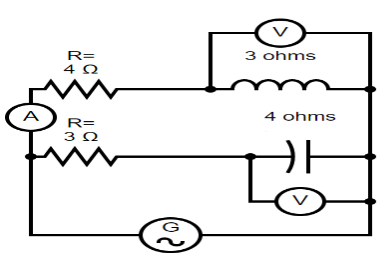
Consider the $AC$ circuit shown and mark the correct option is,
A. Phase difference between ${i_1}$ and ${i_2}$ is $\dfrac{\pi }{2}$
B. Reading of voltmeter ${V_1}$ is $6\sqrt 2 V$
C. Reading of voltmeter ${V_2}$is $- 8\sqrt 2 V$
D. Reading of ammeter is $2\sqrt 2 A$

\varepsilon = {\varepsilon _ \circ }\sin \omega t \\\ {\varepsilon _ \circ } = 20 \\\

Answer 1

In the given diagram we have to show the correct $AC$ circuit and choose the correct option from the given options. In the above diagram we have voltmeter, ammeter and current ${i_1}$ and current ${i_2}$ is passing through in it.

Complete step by step answer:
When current ${i_2}$ is passing through the ammeter we have, $R = 4\Omega$ and ${X_L} = 3\Omega$ in voltmeter ${V_2}$. When current ${i_1}$ is passing then we have, $R = 3\Omega$ and ${X_C} = 4\Omega$ in voltmeter ${V_1}$.Based on this information we are going to identify the AC circuit,That means, in current ${i_1} = 2\sqrt 2$
Whereas the voltmeter is, ${V_2} = {i_1} \times {X_C}$

For the above equation we already have all the values for substituting,
By substituting those values in voltmeter ${V_2}$ we get,
${V_2} = 2\sqrt 2 \times 4 \\\ \Rightarrow {V_2} = 8\sqrt 2$
In the above given options there is no value of voltmeter that we have calculated.Now we are going to calculate the ${E_{rms}}$ value which means root mean square voltage.
Thus we have ${\varepsilon _ \circ } = 20$
Then, ${E_{rms}} = \dfrac{{20}}{{\sqrt 2 }}$
Which means, ${E_{rms}} = 10\sqrt 2$

Now we are going to calculate the current ${i_2}$ value,
${i_2} = \dfrac{{10\sqrt 2 }}{{\sqrt {{{\left( 4 \right)}^2} + {{\left( 3 \right)}^2}} }} \\\ \Rightarrow {i_2} = \dfrac{{10\sqrt 2 }}{5} \\\ \Rightarrow {i_2} = 2\sqrt 2 \\\$
We have calculated the ${i_2}$ value, now we are going to calculate the voltmeter value ${V_1}$. Here
${V_1} = {i_2} \times 3\Omega \\\ \Rightarrow {V_1} = 2\sqrt 2 \times 3\Omega \\\ \therefore {V_1} = 6\sqrt 2 \,V$
Thus from the given options the correct option is reading of voltmeter ${V_1}$ is $6\sqrt 2 V$.

Hence the correct option is B.

Note: From the given data we have proved the reading of a voltmeter ${V_1}$. For this calculation we have used the derivation of root mean square voltage and current.Current of voltmeter in ${V_2}$ is in positive form but in the given options it has negative sign thus from the given options the correct option of reading voltmeter ${V_1}$ is $6\sqrt 2 V$.