Question

Consider that the value of $\sin x=-\dfrac{24}{25}$, then the value of $\tan x$ is
A. $\dfrac{24}{25}$
B. $-\dfrac{24}{7}$
C. $\dfrac{25}{24}$
D. none of these

Answer 1

We explain the function $\arcsin \left( x \right)$. We express the inverse function of sin in the form of ${{\sin }^{-1}}x$. We get $x={{\sin }^{-1}}\left( -\dfrac{24}{25} \right)$. Thereafter we take the tan ratio of that angle to find the solution. We also use the representation of a right-angle triangle with height and hypotenuse ratio being $\dfrac{24}{25}$ and the angle being $\theta$.

Complete step-by-step solution:
We have $\sin x=-\dfrac{24}{25}$, the angular position is in the fourth quadrant where ratio cos and tan are positive and negative respectively.
This gives in ratio $\sin x=-\dfrac{24}{25}$. We know $\sin x=\dfrac{\text{height}}{\text{hypotenuse}}$.
We can take the representation of a right-angle triangle with height and hypotenuse ratio being $\dfrac{24}{25}$ and the angle being $x$. The height and base were considered with respect to that particular angle $x$.

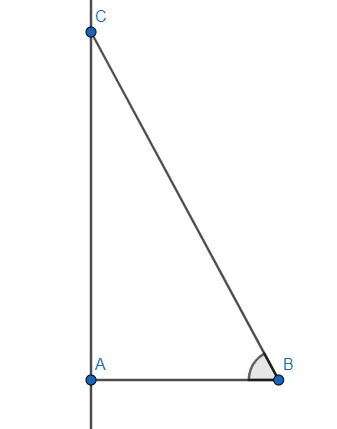
In this case we take $AB=m$ and keeping the ratio in mind we have $AC=24,BC=25$ as the ratio has to be $\dfrac{24}{25}$.
Now we apply the Pythagoras’ theorem to find the length of BC. $B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}$.
So, ${{m}^{2}}=A{{B}^{2}}={{25}^{2}}-{{24}^{2}}=625-576=49$ which gives $AB=7$.
We need to find $\tan x$.
This ratio gives $\tan x=\dfrac{\text{AC}}{\text{AB}}=\dfrac{\text{-24}}{\text{7}}$.
The correct option is B.

Note: We can also apply the trigonometric image form to get the value of $\sin x=-\dfrac{24}{25}$.
It’s given that $\sin x=-\dfrac{24}{25}$ and we need to find $\cos \theta$. We know $\cos \theta =\sqrt{1-{{\sin }^{2}}\theta }$.
Putting the values, we get $\cos \theta =\sqrt{1-{{\sin }^{2}}\theta }=\sqrt{1-{{\left( -\dfrac{24}{25} \right)}^{2}}}=\dfrac{7}{25}$.