Question
Question: Consider lines $L_1: \overrightarrow{r} = \hat{i} + 2\hat{j} + 3\hat{k} + \lambda(2\hat{i} + 3\hat{j...
Consider lines L1:r=i^+2j^+3k^+λ(2i^+3j^+4k^) and L2:2i^+4j^+6k^+μ(3i^+7j^+6k^). If point P, Q lies on the lines L1 and L2 respectively, then PQ CANNOT be parallel to
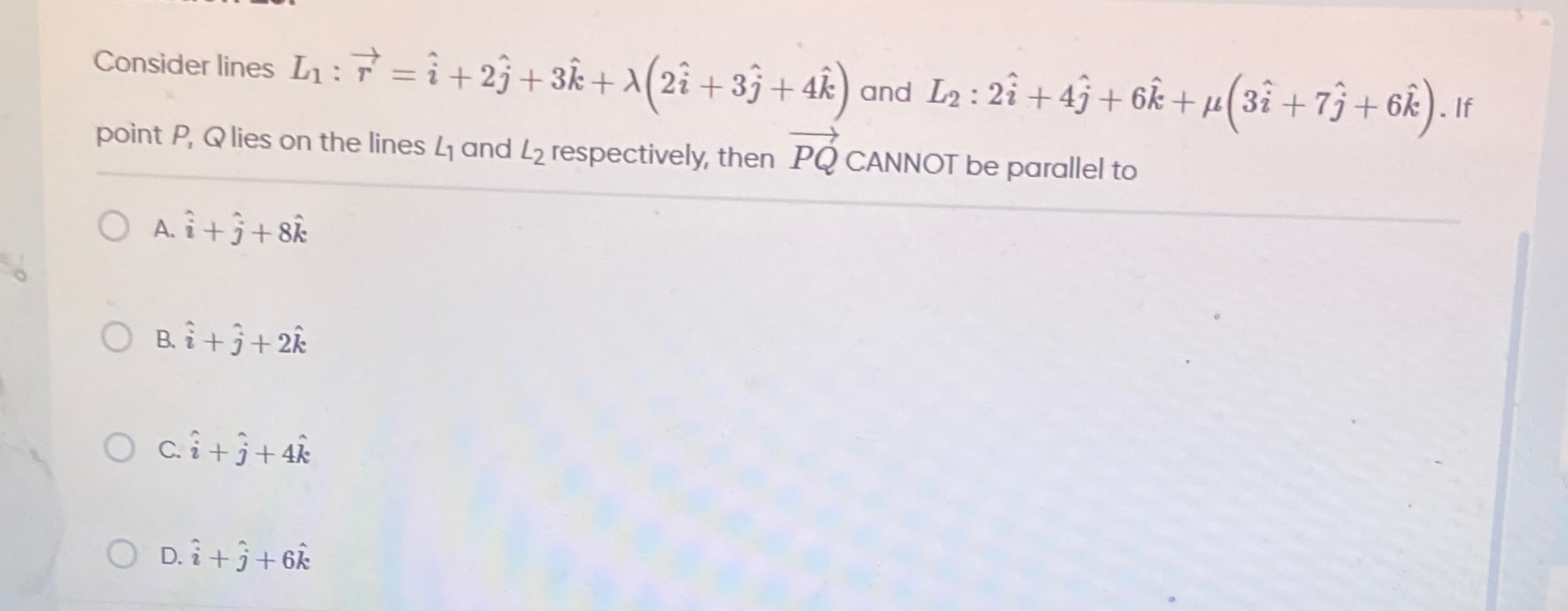
i^+j^+8k^
i^+j^+2k^
i^+j^+4k^
i^+j^+6k^
i^+j^+2k^
Solution
Let P be a point on L1 and Q be a point on L2. The position vectors are: OP=(1+2λ)i^+(2+3λ)j^+(3+4λ)k^ OQ=(2+3μ)i^+(4+7μ)j^+(6+6μ)k^
The vector PQ is given by OQ−OP: PQ=[(2+3μ)−(1+2λ)]i^+[(4+7μ)−(2+3λ)]j^+[(6+6μ)−(3+4λ)]k^ PQ=(1+3μ−2λ)i^+(2+7μ−3λ)j^+(3+6μ−4λ)k^
We can rewrite PQ as: PQ=(i^+2j^+3k^)+μ(3i^+7j^+6k^)−λ(2i^+3j^+4k^)
Let a=i^+2j^+3k^ (the difference between the position vectors of points on L2 and L1). Let d1=2i^+3j^+4k^ (direction vector of L1). Let d2=3i^+7j^+6k^ (direction vector of L2).
So, PQ=a+μd2−λd1.
The vector PQ can be parallel to a vector v if PQ=kv for some scalar k. This implies a+μd2−λd1=kv, or a=kv−μd2+λd1. This means that a must lie in the span of {v,d1,d2}.
First, let's check if a lies in the span of {d1,d2}. This means checking if a=c1d1+c2d2 for scalars c1,c2. i^+2j^+3k^=c1(2i^+3j^+4k^)+c2(3i^+7j^+6k^) Equating coefficients:
- 1=2c1+3c2
- 2=3c1+7c2
- 3=4c1+6c2
Solving equations 1 and 2: Multiply eq 1 by 3 and eq 2 by 2: 3=6c1+9c2 4=6c1+14c2 Subtracting the first from the second: 1=5c2⟹c2=1/5. Substitute c2=1/5 into eq 1: 1=2c1+3(1/5)⟹1=2c1+3/5⟹2/5=2c1⟹c1=1/5.
Now check if these values satisfy eq 3: 4c1+6c2=4(1/5)+6(1/5)=4/5+6/5=10/5=2. Since 2=3, a does NOT lie in the span of {d1,d2}.
Since a is not in the span of {d1,d2}, for a to be in the span of {v,d1,d2}, the vector v must NOT be in the span of {d1,d2}. If v were in the span of {d1,d2}, then the span of {v,d1,d2} would be the same as the span of {d1,d2}, which does not contain a.
Therefore, PQ can be parallel to v if and only if v is NOT in the plane spanned by {d1,d2}. The question asks for which vector PQ CANNOT be parallel to. This means we are looking for a vector v that IS in the span of {d1,d2}.
We check which of the given options is a linear combination of d1 and d2. A vector v is in the span of d1 and d2 if and only if the scalar triple product [v,d1,d2]=0.
Let's test option B: vB=i^+j^+2k^. [vB,d1,d2]=123137246 =13746−12346+22337 =1(18−28)−1(12−12)+2(14−9) =1(−10)−1(0)+2(5) =−10−0+10=0.
Since the scalar triple product is 0, vB is in the span of {d1,d2}. Thus, PQ CANNOT be parallel to i^+j^+2k^.
For completeness, let's check the other options: A. vA=i^+j^+8k^ [vA,d1,d2]=123137846=1(18−28)−1(12−12)+8(14−9)=−10−0+8(5)=30=0.
C. vC=i^+j^+4k^ [vC,d1,d2]=123137446=1(18−28)−1(12−12)+4(14−9)=−10−0+4(5)=10=0.
D. vD=i^+j^+6k^ [vD,d1,d2]=123137646=1(18−28)−1(12−12)+6(14−9)=−10−0+6(5)=20=0.
Therefore, the only vector that lies in the span of d1 and d2 is i^+j^+2k^.
