Question
Question: Consider Lines $L_1: \frac{x-\alpha}{1}=\frac{y}{-2}=\frac{z+\beta}{2}, L_2:x=\alpha, \frac{y}{-\alp...
Consider Lines L1:1x−α=−2y=2z+β,L2:x=α,−αy=2−βz+α, plane P:2x+2: lies in plane P, then
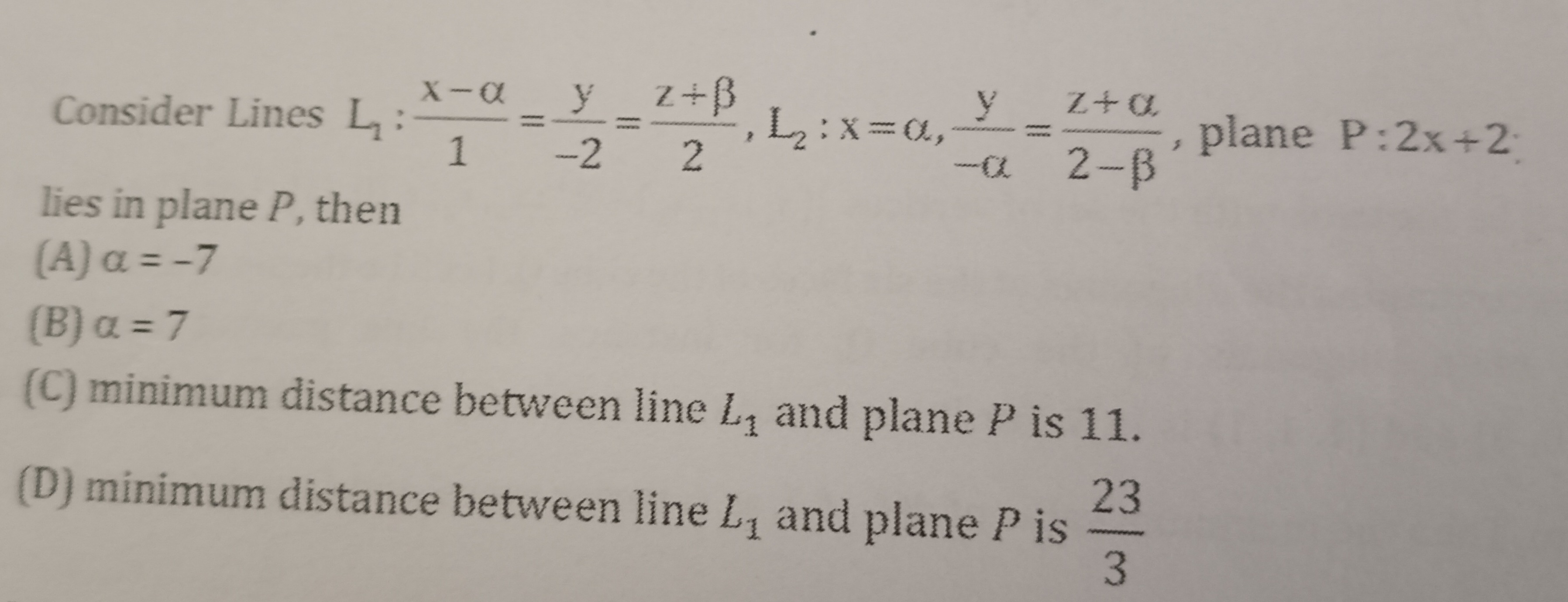
α=−7
α=7
minimum distance between line L1 and plane P is 11.
minimum distance between line L1 and plane P is 323
(A), (B)
Solution
Line L1 lies in plane P if its direction vector is perpendicular to the plane's normal vector AND a point on L1 lies on P. Direction vector of L1: v1=⟨1,−2,2⟩. Assuming the plane equation is P:2x+2y+z=0, its normal vector is n=⟨2,2,1⟩. The dot product v1⋅n=(1)(2)+(−2)(2)+(2)(1)=2−4+2=0. This means L1 is parallel to the plane P. A point on L1 is (α,0,−β). For L1 to lie in P, this point must satisfy the plane equation: 2(α)+2(0)+(−β)=0, which simplifies to β=2α. If a line lies in a plane, the minimum distance between the line and the plane is 0. Therefore, options (C) and (D) are incorrect as they state non-zero distances. Options (A) and (B) propose specific values for α. If α=−7 (Option A), then β=2(−7)=−14, satisfying β=2α. If α=7 (Option B), then β=2(7)=14, also satisfying β=2α. Thus, these are valid scenarios where L1 lies in P.
