Question
Question: Consider $f(x) = \frac{4^x}{4^x+2}$, if $f(\frac{1}{1997})+f(\frac{2}{1997})+ \dots + f(\frac{1996}{...
Consider f(x)=4x+24x, if f(19971)+f(19972)+⋯+f(19971996)=499q, then q is equal to
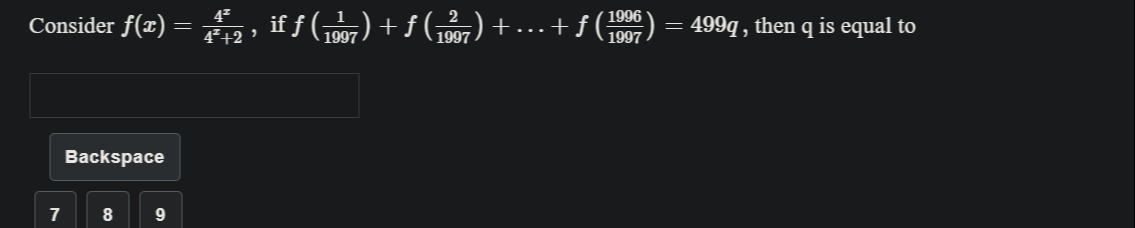
2
Solution
To solve the problem, we first analyze the given function f(x)=4x+24x.
We look for a special property of this function, specifically f(x)+f(1−x).
-
Find f(1−x):
Substitute (1−x) for x in the function definition: f(1−x)=41−x+241−x
We can rewrite 41−x as 4⋅4−x=4x4.
So, f(1−x)=4x4+24x4
To simplify, multiply the numerator and denominator by 4x:
f(1−x)=4+2⋅4x4
Factor out 2 from the denominator:
f(1−x)=2(2+4x)4=2+4x2
-
Calculate f(x)+f(1−x):
Now, add f(x) and f(1−x):
f(x)+f(1−x)=4x+24x+4x+22
Since both terms have the same denominator, we can add the numerators:
f(x)+f(1−x)=4x+24x+2=1
This property, f(x)+f(1−x)=1, is crucial for solving the problem.
-
Evaluate the sum:
The given sum is S=f(19971)+f(19972)+⋯+f(19971996).
Let N=1997. The sum can be written as S=∑k=1N−1f(Nk).
The terms in the sum range from k=1 to k=1996. There are 1996 terms in total.
We can pair the terms using the property f(x)+f(1−x)=1.
Consider a pair of terms f(Nk) and f(NN−k).
Note that NN−k=1−Nk.
So, f(Nk)+f(NN−k)=f(Nk)+f(1−Nk)=1.
The terms in the sum can be paired as follows:
(f(19971)+f(19971996))+(f(19972)+f(19971995))+…
Since there are 1996 terms, and 1996 is an even number, all terms can be perfectly paired.
The number of such pairs is 21996=998.
Each pair sums to 1.
Therefore, the total sum S=998×1=998.
-
Solve for q:
We are given that the sum S=499q.
We found S=998.
So, 998=499q.
To find q, divide both sides by 499:
q=499998
q=2
The final answer is 2.
Explanation of the solution:
The function f(x)=4x+24x possesses the property f(x)+f(1−x)=1. This is derived by simplifying f(1−x) to 4x+22 and adding it to f(x). The given sum consists of 1996 terms of the form f(1997k). By pairing terms f(1997k) with f(19971997−k), each pair sums to f(1997k)+f(1−1997k)=1. Since there are 1996 terms, there are 1996/2=998 such pairs. Thus, the total sum is 998×1=998. Equating this to 499q, we get 998=499q, which yields q=2.
