Question

Consider functions $f$ and $g$ such that composite $g \circ f$ is defined and is one are $g$ both necessarily one-one?

Answer 1

Here in this question, we need to check whether both $g \circ f$ and $g$ is necessarily one-one or not. For this, first we need to consider a set of functions $f$ and $g$ and further define a composition function $g \circ f$ then check the one-one condition to get the required solution.

Complete step by step answer:
Let’s consider a two functions $f\left( x \right)$ and $g\left( x \right)$, then function $f$ ranges from $f:A \to B$ and $g$ ranges from $g:B \to C$.
Now, the composite function $g$ and $f$ $g \circ f:A\because C$, then defined as $g \circ f:A \to C$ is one-one.
Now, we are to prove that $f$ is one -one if possible. Suppose, that $f$ is not one-one.
Let there exists a ${x_1}$, ${x_2}$ $\in A$ such that ${x_1} \ne {x_2}$ But $f\left( {{x_1}} \right) = f\left( {{x_2}} \right)$, then
$\Rightarrow \,\,\,\,g\left( {f\left( {{x_1}} \right)} \right) = g\left( {f\left( {{x_2}} \right)} \right)$
Then,
$\Rightarrow \,\,\,\,g \circ f\left( {{x_1}} \right) = g \circ f\left( {{x_2}} \right)$
Therefore, ${x_1}$, ${x_2}$ $\in A$ such that ${x_1} \ne {x_2}$ but $g \circ f\left( {{x_1}} \right) = g \circ f\left( {{x_2}} \right)$.
Therefore, $g \circ f$ is not one which is against the given hypothesis that $g$ of is one -one superposition is wrong.

Now, let f:\left\\{ {1,2,3,4} \right\\} \to \left\\{ {1,2,3,4,5,6} \right\\}

$f$ is one-one and g:\left\\{ {1,2,3,4,5,6} \right\\} \to \left\\{ {1,2,3,4,5,6} \right\\}

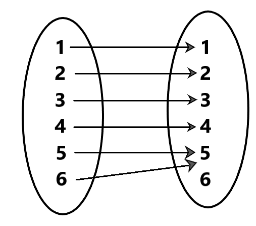
$g$ is not one-one. The composite function $g \circ f$

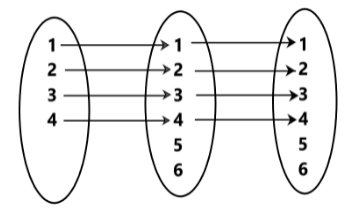
Hence, which shows that $g \circ f$ is one-one. $f$ and $g$ are not necessarily one-one.

Note: One to one function basically denotes the mapping between the two sets. A function $g$ is one-to-one if every element of the range of g corresponds to exactly one element of the domain of $g$. A function $f:A \to B$ is said to be an onto function if $f\left( A \right)$, the image of A equal to B. that is $f$ is onto if every element of B the co-domain is the image of at least one element of A the domain.