Question

Consider following phase diagram. If for the solution value of x is 2.5 Kelvin while that of y is 5 Kelvin then value of $K_f/K_b$ for the solvent is __________. [Assume that the van't Hoff factor 'i' is independent of temperature]

Answer 1

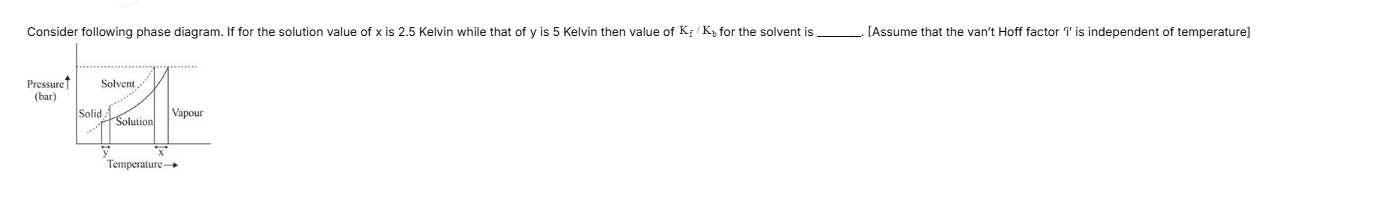
2

Answer 2

The phase diagram shows the phase boundaries for a pure solvent and a solution. The freezing point of the pure solvent is the temperature at which the solid and liquid phases are in equilibrium at a given pressure. The boiling point of the pure solvent is the temperature at which the liquid and vapor phases are in equilibrium at a given pressure.

When a non-volatile solute is added to a solvent, the freezing point of the solution is lowered (freezing point depression, $\Delta T_f$), and the boiling point of the solution is raised (boiling point elevation, $\Delta T_b$).

From the phase diagram, at a constant pressure (represented by the horizontal line), the difference between the freezing point of the pure solvent and the freezing point of the solution is denoted by 'y'. This difference is the freezing point depression, so $\Delta T_f = y$. The difference between the boiling point of the solution and the boiling point of the pure solvent is denoted by 'x'. This difference is the boiling point elevation, so $\Delta T_b = x$.

We are given that for the solution, the value of x is 2.5 Kelvin and that of y is 5 Kelvin. So, $\Delta T_b = x = 2.5$ K and $\Delta T_f = y = 5$ K.

The colligative properties are related to the molality of the solution by the following equations: Freezing point depression: $\Delta T_f = i K_f m$ Boiling point elevation: $\Delta T_b = i K_b m$ where $i$ is the van't Hoff factor, $K_f$ is the cryoscopic constant, $K_b$ is the ebullioscopic constant, and $m$ is the molality of the solution.

We are given that the van't Hoff factor 'i' is independent of temperature. Since we are considering the same solution, the molality 'm' is also the same for both the freezing point depression and boiling point elevation.

Using the given values and the formulas: $5 = i K_f m$ (Equation 1) $2.5 = i K_b m$ (Equation 2)

We want to find the value of $K_f/K_b$. We can divide Equation 1 by Equation 2: $\frac{5}{2.5} = \frac{i K_f m}{i K_b m}$

Since $i$ and $m$ are the same and non-zero, they cancel out: $\frac{5}{2.5} = \frac{K_f}{K_b}$ $2 = \frac{K_f}{K_b}$

Thus, the value of $K_f/K_b$ for the solvent is 2.

Explanation of the solution: The freezing point depression ($\Delta T_f$) and boiling point elevation ($\Delta T_b$) are colligative properties given by $\Delta T_f = i K_f m$ and $\Delta T_b = i K_b m$. From the phase diagram and the problem statement, $\Delta T_f = y = 5$ K and $\Delta T_b = x = 2.5$ K. For the same solution, $i$ and $m$ are constant. Dividing the equations, we get $\frac{\Delta T_f}{\Delta T_b} = \frac{i K_f m}{i K_b m} = \frac{K_f}{K_b}$. Substituting the values, $\frac{5}{2.5} = \frac{K_f}{K_b}$, which gives $\frac{K_f}{K_b} = 2$.