Question

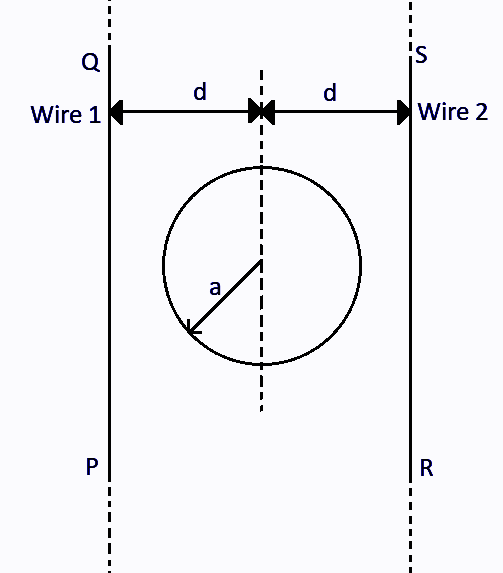
Consider $d \gg a$ , and the loop is rotated about its diameter parallel to the wires by $30^\circ$ from the position shown in the figure. If the currents in the wires are in the opposite directions, the torque on the loop at its new position will be (assume that the net field due to the wires is constant over the loop)

(A) $\dfrac{{{\mu _o}{I^2}{a^2}}}{d}$
(B) $\dfrac{{{\mu _o}{I^2}{a^2}}}{{2d}}$
(C) $\dfrac{{\sqrt 3 {\mu _o}{I^2}{a^2}}}{d}$
(D) $\dfrac{{\sqrt 3 {\mu _o}{I^2}{a^2}}}{{2d}}$

Answer 1

Hint The torque is given by the cross product of the magnetic dipole moment of the loop and the magnetic field. The angle between the dipole moment and the magnetic field is given in the question as $30^\circ$ . So substituting the values we get the torque.

Formula Used: In this solution we will be using the following formula,
$\Rightarrow \vec \tau = \vec M \times \vec B$
where $\vec \tau$ is the torque, $\vec M$ is the magnetic dipole moment and $\vec B$ is the magnetic field.

Complete step by step answer
In the question we are provided that the loop is rotated along its diameter by $30^\circ$ . Now initially the direction of the area vector of the loop and the direction of the magnetic field due to the wires was the same. So there was no torque acting on it. But on rotating the wire by $30^\circ$ the angle between the vector of the loop and the magnetic field becomes $30^\circ$ .
Therefore, there is a torque acting on the loop. Now, this torque is given by the formula,
$\Rightarrow \vec \tau = \vec M \times \vec B$
We can break this equation as,
$\Rightarrow \tau = MB\sin \theta$
Here $\theta$ is $30^\circ$ so $\sin 30 = \dfrac{1}{2}$
Now the magnetic dipole moment is given as,
$\Rightarrow \vec M = I\vec A$ where $I$ is the current and $\vec A$ is the area. It is given in the question that the loop has a radius of $a$ . So the area of the loop will be $A = \pi {a^2}$ .
So the magnetic moment is, $M = I\pi {a^2}$
The magnetic field caused due to a current carrying at a distance $d$ from the wire is given by the formula,
$\Rightarrow {\vec B_o} = \dfrac{{{\mu _o}I}}{{2\pi d}}$
It is said that the wires are carrying current in the opposite directions. So the magnetic field will be in the same direction for both the wires. Therefore,
$\Rightarrow \vec B = \dfrac{{2{\mu _o}I}}{{2\pi d}}$
Cancelling the 2 we get,
$\Rightarrow \vec B = \dfrac{{{\mu _o}I}}{{\pi d}}$
Now substituting all the values in the equation for the torque we get,
$\Rightarrow \tau = I\pi {a^2} \times \dfrac{{{\mu _o}I}}{{\pi d}} \times \dfrac{1}{2}$
Therefore on arranging we get,
$\Rightarrow \tau = \dfrac{{{\mu _o}{I^2}{a^2}}}{{2d}}$
Therefore the correct option is B.

Note
Since the torque is the cross product of the magnetic dipole moment and the magnetic field, the direction of the torque will be perpendicular to both the magnetic moment and the field. This direction will be given by the right hand rule for the cross products.