Question

Consider complex numbers z and w satisfying the equation $z+w=\frac{\overline{z}}{w}$ and $\frac{1}{w}+z=w\overline{z}$, then which of the following is/are correct?

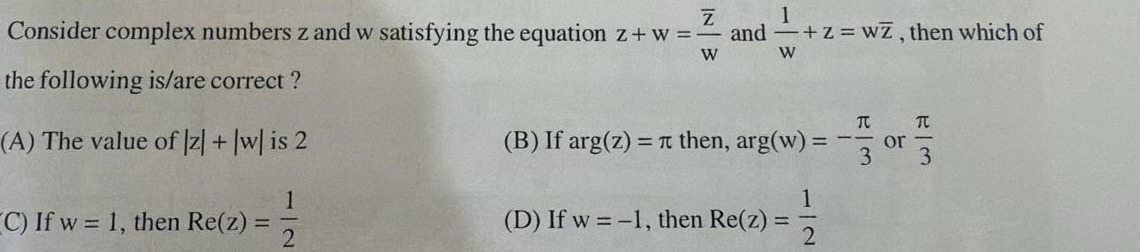
• A. The value of $|z| + |w|$ is 2
• B. If arg(z) = $\pi$ then, arg(w) = $-\frac{\pi}{3}$ or $\frac{\pi}{3}$
• C. If w = 1, then Re(z) = $\frac{1}{2}$
• D. If w = -1, then Re(z) = $\frac{1}{2}$

Answer 1

Answer: (B), (C), (D)

(B), (C), (D)

Answer 2

Let the given equations be:

1. $z+w=\frac{\overline{z}}{w}$

2. $\frac{1}{w}+z=w\overline{z}$

Assume $w \neq 0$. Multiply both equations by $w$:

1') $zw + w^2 = \overline{z}$

2') $1 + zw = w^2\overline{z}$

Subtract equation (1') from equation (2'):

$(1 + zw) - (zw + w^2) = w^2\overline{z} - \overline{z}$

$1 - w^2 = \overline{z}(w^2 - 1)$

$1 - w^2 = -\overline{z}(1 - w^2)$

$(1 - w^2) + \overline{z}(1 - w^2) = 0$

$(1 - w^2)(1 + \overline{z}) = 0$

This implies either $1 - w^2 = 0$ or $1 + \overline{z} = 0$.

Case 1: $1 + \overline{z} = 0$

This means $\overline{z} = -1$, so $z = -1$.

Substitute $z=-1$ into the original equations.

Eq 1: $-1+w = \frac{-1}{w}$

$-w+w^2 = -1$

$w^2 - w + 1 = 0$

The solutions are $w = \frac{1 \pm \sqrt{1-4}}{2} = \frac{1 \pm i\sqrt{3}}{2}$.

These are $e^{i\pi/3}$ and $e^{-i\pi/3}$. Let's check if these values of $w$ satisfy Eq 2 with $z=-1$.

Eq 2: $\frac{1}{w} + (-1) = w(-1)$

$\frac{1}{w} - 1 = -w$

$\frac{1}{w} + w = 1$

If $w = \frac{1+i\sqrt{3}}{2} = e^{i\pi/3}$, then $\frac{1}{w} = \overline{w} = \frac{1-i\sqrt{3}}{2} = e^{-i\pi/3}$.

$\frac{1}{w} + w = \frac{1-i\sqrt{3}}{2} + \frac{1+i\sqrt{3}}{2} = \frac{2}{2} = 1$. This is satisfied.

If $w = \frac{1-i\sqrt{3}}{2} = e^{-i\pi/3}$, then $\frac{1}{w} = \overline{w} = \frac{1+i\sqrt{3}}{2} = e^{i\pi/3}$.

$\frac{1}{w} + w = \frac{1+i\sqrt{3}}{2} + \frac{1-i\sqrt{3}}{2} = \frac{2}{2} = 1$. This is satisfied.

So, one set of solutions is $z=-1$ and $w = e^{\pm i\pi/3}$.

Case 2: $1 - w^2 = 0$

This means $w^2 = 1$, so $w = 1$ or $w = -1$.

Subcase 2a: $w=1$.

Substitute $w=1$ into the original equations.

Eq 1: $z+1 = \frac{\overline{z}}{1} \implies z+1 = \overline{z}$.

Let $z = x+iy$. $x+iy+1 = x-iy$.

$x+1+iy = x-iy$.

Comparing real and imaginary parts:

$x+1 = x \implies 1=0$, which is a contradiction.

$y = -y \implies 2y=0 \implies y=0$.

Since we have a contradiction ($1=0$), there is no solution for $z$ when $w=1$.

Subcase 2b: $w=-1$.

Substitute $w=-1$ into the original equations.

Eq 1: $z+(-1) = \frac{\overline{z}}{-1} \implies z-1 = -\overline{z} \implies z+\overline{z} = 1$.

Let $z=x+iy$. $(x+iy)+(x-iy) = 1 \implies 2x = 1 \implies x = 1/2$.

So $Re(z) = 1/2$. $z = 1/2 + iy$ for any real $y$.

Eq 2: $\frac{1}{-1} + z = (-1)\overline{z} \implies -1+z = -\overline{z} \implies z+\overline{z} = 1$.

This is the same equation obtained from Eq 1.

So, the second set of solutions is $w=-1$ and $z$ is any complex number with $Re(z)=1/2$.

The possible solutions $(z,w)$ are:

1. $z=-1$ and $w \in \{e^{i\pi/3}, e^{-i\pi/3}\}$

2. $w=-1$ and $Re(z)=1/2$

Now let's check the options:

(A) The value of $|z| + |w|$ is 2.

For solutions from Case 1: $z=-1$, $|z|=1$. $w=e^{\pm i\pi/3}$, $|w|=1$. $|z|+|w|=1+1=2$.

For solutions from Case 2: $w=-1$, $|w|=1$. $z=1/2+iy$, $|z|=\sqrt{(1/2)^2+y^2} = \sqrt{1/4+y^2}$.

$|z|+|w| = \sqrt{1/4+y^2}+1$.

This value is 2 only if $\sqrt{1/4+y^2}=1$, which means $1/4+y^2=1$, $y^2=3/4$, $y=\pm \sqrt{3}/2$.

For example, if $z=1/2$ (i.e., $y=0$), then $|z|=1/2$, $|w|=1$, and $|z|+|w|=3/2 \neq 2$.

So, option (A) is not true for all solutions.

(B) If arg(z) = $\pi$ then, arg(w) = $-\frac{\pi}{3}$ or $\frac{\pi}{3}$.

If $\arg(z)=\pi$, then $z$ is a negative real number. From our solutions, $z=-1$ is a negative real number with $\arg(z)=\pi$.

When $z=-1$, the possible values for $w$ are $e^{i\pi/3}$ and $e^{-i\pi/3}$.

The arguments of these values are $\pi/3$ and $-\pi/3$ (modulo $2\pi$).

So, if $\arg(z)=\pi$ (which implies $z=-1$), then $\arg(w) = \pi/3$ or $-\pi/3$.

This option is correct.

(C) If w = 1, then Re(z) = $\frac{1}{2}$.

We found in Subcase 2a that $w=1$ yields no solutions for $z$.

The premise "If w=1" is false, as $w$ cannot be 1 for any solution. A conditional statement "If P then Q" is considered true if the premise P is false.

Thus, option (C) is correct.

(D) If w = -1, then Re(z) = $\frac{1}{2}$.

We found in Subcase 2b that if $w=-1$, then $z$ must satisfy $Re(z)=1/2$.

This option is correct.

The correct options are (B), (C), and (D).