Question

Consider an "L”-shaped object where the vertical leg extends from the origin to $(0,5)$ and the horizontal segment extends from the origin to $(3,0)$. Assume that the object has uniform linear density throughout. Where is the location of the center of mass (CoM )?
A. $(1.5,1.5)$
B. $(1.5,2.5)$
C. $(2.5,2.5)$
D. The center of mass for an "L” is undefined because there is no single point on the object where it can be supported, such that it will not rotate
E. None of these

Answer 1

The Centre of mass of any object is a point on the object with respect to that point we can imagine the object as a point with the whole mass located at that position. If a force is applied to this point the object will have linear acceleration without any angular momentum.

Formula used:
The centre of mass of a one dimensional object is given by,
${x_{CM}} = \dfrac{{\sum\limits_i {{m_i}{x_i}} }}{M}$
where, ${x_{CM}}$ is the centre of mass of the body, ${m_i}$ is the mass of the $ith$ particle, ${x_i}$ is the position of $ith$ particle from origin and $M$ is the total mass.
For continuous object the centre of mass is
${x_{CM}} = \dfrac{{\int {xdm} }}{{\int {dm} }}$
where, $x$ is the position of the elementary mass $dm$.

Complete step by step answer:
We have given here a L-shaped one dimensional object. Now, we have to find the centre of mass of the object with respect to the origin. So, to find the centre of mass of it we will divide it into two parts and determine the centre of mass of each part and then find the centre of mass of the object using that. Now, for continuous object the centre of mass is
${x_{CM}} = \dfrac{1}{M}\int {xdm}$
where, $x$ is the position of the elementary mass $dm$.

Let the linear mass density of the object is $\rho$.

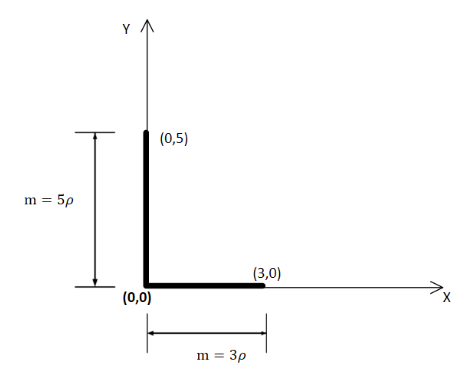
So, the centre of mass of the horizontal part is,
${x_{CM}} = \dfrac{{\int {x\rho dx} }}{{\int {dm} }}$ [since, $dm = \rho dx$]
$\Rightarrow {x_{CM}} = \dfrac{{\rho \int {xdx} }}{{\rho \int {dx} }}$
$\Rightarrow {x_{CM}} = \dfrac{{\int\limits_0^3 {xdx} }}{{\int\limits_0^3 {dx} }}$
Putting the limits of the x axis,
${x_{CM}} = \dfrac{{\left. {\dfrac{{{x^2}}}{2}} \right|_0^3}}{{\left. x \right|_0^3}}$
$\Rightarrow {x_{CM}} = \dfrac{1}{3}(\dfrac{{{3^2}}}{2} - \dfrac{{{0^2}}}{2})$
$\Rightarrow {x_{CM}} = \dfrac{3}{2}$

So, the centre of mass of the vertical part is,
${y_{CM}} = \dfrac{{\int {y\rho dy} }}{{\int {dm} }}$ [since, $dm = \rho dx$]
$\Rightarrow {y_{CM}} = \dfrac{{\rho \int {ydy} }}{{\rho \int {dy} }}$
$\Rightarrow {y_{CM}} = \dfrac{{\int\limits_0^5 {ydy} }}{{\int\limits_0^5 {dy} }}$
$\Rightarrow {y_{CM}} = \dfrac{{\left. {\dfrac{{{y^2}}}{2}} \right|_0^5}}{{\left. y \right|_0^5}}$
$\Rightarrow {y_{CM}} = \dfrac{1}{5}(\dfrac{{{5^2}}}{2} - \dfrac{{{0^2}}}{2})$
$\Rightarrow {y_{CM}} = \dfrac{5}{2}$

Now, these two part will make the whole object so, the x coordinate of the centre of mass of the whole object will be,
${x_{CM}} = \dfrac{{(3\rho )\dfrac{3}{2} + (5\rho )0}}{{3\rho + 5\rho }}$
[mass of the vertical part is $5\rho$ and x coordinate is at origin, mass of the horizontal part is $3\rho$]
${x_{CM}} = \dfrac{{\dfrac{{9\rho }}{2}}}{{8\rho }}$
$\Rightarrow {x_{CM}} = \dfrac{9}{{16}}$

And the y coordinate of the centre of mass of the whole object will be,
${y_{CM}} = \dfrac{{(3\rho )0 + (5\rho )\dfrac{5}{2}}}{{3\rho + 5\rho }}$
$\Rightarrow {y_{CM}} = \dfrac{{\dfrac{{25\rho }}{2}}}{{8\rho }}$
$\therefore {y_{CM}} = \dfrac{{25}}{{16}}$
Hence, the centre of mass of the object will be at, $(\dfrac{9}{{16}},\dfrac{{25}}{{16}})$. Hence, none of the options have the correct answer.

Hence, option E is the correct answer.

Note: When calculating the centre of mass of the object with the horizontal and vertical parts keep in mind that the one of the components is at origin when calculating the x or y coordinate of the centre of mass of the object.