Question
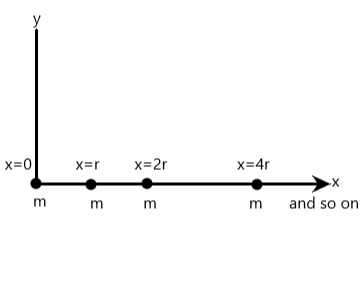
Question: Consider an infinite distribution of point masses (each of mass \[m\]) placed on the x axis as shown...
Consider an infinite distribution of point masses (each of mass m) placed on the x axis as shown in the diagram. What is the gravitational force acting on the point mass placed at the origin?
A. 3r24Gm2
B. 3r2Gm2
C. r24Gm2
D. r2Gm2
Solution
We need to use Newton's universal law of gravitation to find the force on the mass at the origin due to the other individual masses on the x axis. The sum of the forces is a geometric progression with a sum to infinity.
Formula used: In this solution we will be using the following formulae;
F=r2Gm1m2 where F is the gravitational force of attraction between two bodies, m1 and m2 are the masses of the two bodies, and r is the distance between them (their centres for non-point masses).
S∞=1−ra for 0<r<1 where S∞ is the sum to infinity of a geometric seriesa is the first term of the series and r is the common ratio.
Complete step by step answer:
We see an infinite arrangement of point masses and we are to find the force due to this infinite array on the mass at the origin.
To do so, we use the Newton’s law which mathematically can be given as
F=r2Gm1m2 where F is the gravitational force of attraction between two bodies, m1 and m2 are the masses of the two bodies, and r is the distance between them.
Hence, we have for the first mass to be
F1=r2Gmm
Similarly for the second mass on the origin mass we have
F2=(2r)2Gmm=4r2Gmm
Also, for the third mass
F3=(4r)2Gmm=16r2Gmm
But the force is the sum of all the individual forces as in
F=F1+F2+F3+... since it continues to infinity.
Hence, we have that
⇒F=r2Gmm[11+41+161+...]
If observed, the sum in the bracket is a geometric progression with a common ratio of 41
Also, the sum to infinity of a geometric progression can be given as
S∞=1−ra for 0<r<1 where a is the first term of the series and r is the common ratio. Hence inserting known values
S∞=1−411
⇒S∞=1−411=431=34.
Hence,
F=r2Gmm[34]
⇒F=3r24Gm2
Hence, the correct option is A.
Note: Note that in actuality, the masses cannot be to a literal infinity. The term infinity is used in this case to denote that the masses are numerous. Also, the common ratio is gotten from dividing any of the term by the preceding term as in
r=41÷1=161÷41=41
