Question

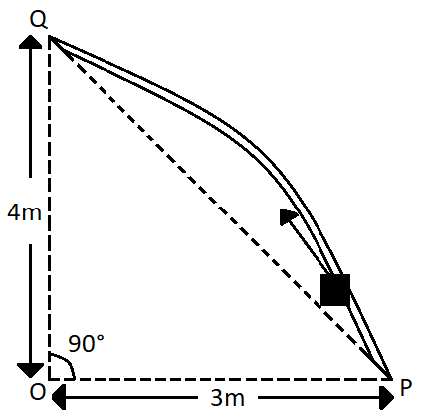
Consider an elliptically shaped rail PQ in the vertical plane with OP $= 3m$ and OQ $= 4m$ . A block of mass $1kg$ is pulled along the rail from P to Q with a force of $18N$ , which is always parallel to line PQ (see the figure given). Assuming no frictional losses, the kinetic energy of the block when it reaches Q is $\left( {n \times 10} \right)$ Joules. The value of $n$ is (take acceleration due to gravity $= 10m{s^{ - 2}}$ )

Answer 1

Hint From the figure we can calculate the displacement of the particle from the point P to the point Q. So we can then calculate the work done. The work done will be equal to the total energy at Q. We can calculate the PE at Q according to its height. The kinetic energy will be the difference between the work done and the potential energy.

Formula Used: In this solution we will be using the following formula,
$\Rightarrow W = \vec F \cdot \vec S$
where $W$ is the work done, $\vec F$ is the force and $\vec S$ is the displacement.

Complete step by step answer
According to the question, a block is taken from the point P to the point Q along the elliptical path PQ. Now the force acting on the block produces work on it. So this work done will depend on the displacement of the block irrespective of the path that is followed by the block. SO the displacement of the block will be the hypotenuse of the triangle POQ.
Therefore, we have,
$\Rightarrow PQ = \sqrt {{3^2} + {4^2}}$
On calculating we get the value as,
$\Rightarrow PQ = \sqrt {9 + 16}$
On adding and removing the square root we get,
$\Rightarrow S = PQ = \sqrt {25} = 5m$
This is the displacement of the block.
Now the force that is acting on the block is in the same direction as the displacement. So the angle between the force and the displacement is 0. Now the work done is given by,
$\Rightarrow W = \vec F \cdot \vec S$
This gives us,
$\Rightarrow W = FS\cos 0$
Since $\cos 0$ is equal to 1 and the force is given as, $F = 18N$ , substituting we get,
$\Rightarrow W = 18 \times 5$
That is equal to,
$\Rightarrow W = 90J$
Now the potential energy of the block is given by the formula,
$\Rightarrow PE = mgh$
The mass of the block is $m = 1kg$ , $g = 10m{s^{ - 2}}$ is given and the height of the point Q is given in the diagram to be, $h = 4m$
So substituting the values we get,
$\Rightarrow PE = 1 \times 10 \times 4$
So we get the potential energy as,
$\Rightarrow PE = 40J$
Now the kinetic energy of the block will be the difference in the work done and the potential energy. So we get,
$\Rightarrow KE = W - PE$
Substituting the values we have,
$\Rightarrow KE = \left( {90 - 40} \right) = 50J$
Now we can also write it as,
$\Rightarrow KE = \left( {5 \times 10} \right)J$
So comparing the form $\left( {n \times 10} \right)$ in the question, we have the value of $n$ as 5.

Note
Here in order to calculate the kinetic energy of the block we have taken the work done on the block as the total energy of the block which is divided into its kinetic energy and its potential energy. Since the force acting on the body is conservative in nature, so the work done is independent of the path followed by the body.