Question

Consider an ellipse, whose centre is at the origin and its major axis is along the x – axis. If its eccentricity is $\dfrac{3}{5}$ and the distance between its foci is 6, then the area (in sq. units) of the quadrilateral inscribed in the ellipse, with the vertices as the vertices of the ellipse, is.
(a) 80
(b) 8
(c) 40
(d) 32

Answer 1

To solve this question, we need to find the major axis and minor axis of ellipse. To find these values, we will use various relations concerned with ellipse available with us. Suppose the horizontal vertices of the ellipse with centre at origin are (a, 0) and (─a, 0) and the vertical vertices are (b, 0) and (─b, 0), one of the relations is distance between the foci = 2ae, where e is the eccentricity of the ellipse. Another relation available with us is ${{b}^{2}}={{a}^{2}}\left( 1-{{e}^{2}} \right)$. Thus, we can find the values of a and b and thus twice of these values will be the length of major and minor axes. Once we get a and b, we will draw a figure and draw a quadrilateral with the vertices as the vertices of the ellipse. The major and minor axes thus will be its diagonal. We know that the area of a kite is given as $\dfrac{1}{2}{{d}_{1}}{{d}_{2}}$, where ${{d}_{1}}$ and ${{d}_{2}}$ are its diagonals.

Complete step by step answer:
The eccentricity of the ellipse is given as $e=\dfrac{3}{5}$.
We know that the distance between the foci is given by the relation 2ae.
It is given to us that the distance between the foci is 6.
$\begin{aligned} & \Rightarrow 6=2a\left( \dfrac{3}{5} \right) \\\ & \Rightarrow a=5 \\\ \end{aligned}$
Now, we know another relation of ellipse given as ${{b}^{2}}={{a}^{2}}\left( 1-{{e}^{2}} \right)$. We will substitute values of a and e in this relation.
$\begin{aligned} & \Rightarrow {{b}^{2}}={{\left( 5 \right)}^{2}}\left( 1-{{\left( \dfrac{3}{5} \right)}^{2}} \right) \\\ & \Rightarrow {{b}^{2}}=16 \\\ & \Rightarrow b=4 \\\ \end{aligned}$
Therefore, the value of a is 5 and value of b = 4.
Thus, the length of the major axis will be twice the value of a.
So, length of major axis = 2(5) = 10
Similarly, the length of the minor axis will be twice the value of b.
So, length of minor axis = 2(4) = 8
Now, with this information, we will find the figure of the ellipse and inscribe a quadrilateral inside the ellipse with its vertices as the vertices of the ellipse.

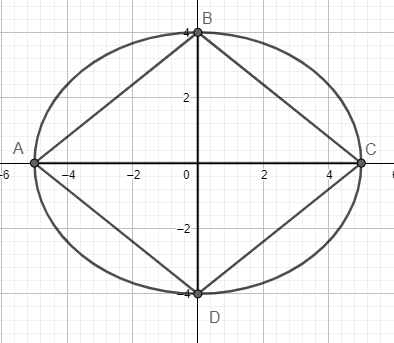
The major and minor axes of the ellipse act as the diameter of the quadrilateral ABCD. We can see that the quadrilateral thus formed is a kite.
We know that the area of a kite is given as half the product of its diameter.
$\begin{aligned} & \Rightarrow A=\dfrac{1}{2}{{d}_{1}}{{d}_{2}} \\\ & \Rightarrow A=\dfrac{1}{2}\left( AC \right)\left( BD \right) \\\ & \Rightarrow A=\dfrac{1}{2}\left( 10 \right)\left( 8 \right) \\\ & \Rightarrow A=40 \\\ \end{aligned}$
Therefore, the area of the ellipse is 40 sq units.

So, the correct answer is “Option A”.

Note: The foci of the ellipse have the coordinates $\left( \pm ae,0 \right)$. Thus, the distance between the foci is 2ae. Students can directly remember the above relations as they are true for all ellipses. It is also advised to draw a figure whenever possible. Figure gives insights which are usually overlooked during textual information.