Question

Consider an electron in the $n = 3$ orbit of a hydrogen-like atom with atomic number $Z$. At absolute temperature $T$, a neutron having thermal energy $k_BT$ has the same de Broglie wavelength as that of this electron. If this temperature is given by $T = \frac{Z^2h^2}{\alpha \pi^2 a_0^2 m_N k_B}$, (where $h$ is the Planck's constant, $k_B$ is the Boltzmann constant, $m_N$ is the mass of the neutron and $a_0$ is the first Bohr radius of hydrogen atom) then the value of $\alpha$ is ______

Answer 1

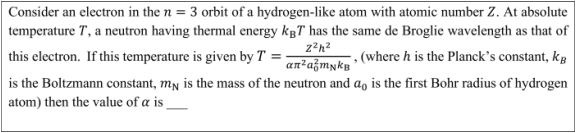
72

Answer 2

The de Broglie wavelength of an electron in the $n$-th orbit of a hydrogen-like atom with atomic number $Z$ is given by $\lambda_e = \frac{2\pi r_n}{n}$, where $r_n$ is the radius of the $n$-th orbit. The radius of the $n$-th orbit is $r_n = \frac{n^2 a_0}{Z}$, where $a_0$ is the first Bohr radius of hydrogen.

So, the de Broglie wavelength of the electron in the $n$-th orbit is $\lambda_e = \frac{2\pi}{n} \left(\frac{n^2 a_0}{Z}\right) = \frac{2\pi n a_0}{Z}$.

For $n=3$, the de Broglie wavelength of the electron is $\lambda_e = \frac{2\pi (3) a_0}{Z} = \frac{6\pi a_0}{Z}$.

The de Broglie wavelength of a particle with kinetic energy $E$ is given by $\lambda = \frac{h}{p} = \frac{h}{\sqrt{2mE}}$.

The neutron has thermal energy $k_BT$. So, the kinetic energy of the neutron is $E_N = k_BT$.

The de Broglie wavelength of the neutron is $\lambda_N = \frac{h}{\sqrt{2 m_N k_B T}}$.

According to the problem statement, the de Broglie wavelengths are the same: $\lambda_e = \lambda_N$.

$\frac{6\pi a_0}{Z} = \frac{h}{\sqrt{2 m_N k_B T}}$.

We are given the temperature $T = \frac{Z^2h^2}{\alpha \pi^2 a_0^2 m_N k_B}$. Substitute this expression for $T$ into the equation:

$\frac{6\pi a_0}{Z} = \frac{h}{\sqrt{2 m_N k_B \left(\frac{Z^2h^2}{\alpha \pi^2 a_0^2 m_N k_B}\right)}}$.

The terms $m_N$ and $k_B$ cancel out in the denominator inside the square root:

$\frac{6\pi a_0}{Z} = \frac{h}{\sqrt{\frac{2 Z^2 h^2}{\alpha \pi^2 a_0^2}}}$.

Simplify the square root in the denominator:

$\sqrt{\frac{2 Z^2 h^2}{\alpha \pi^2 a_0^2}} = \sqrt{\frac{2}{\alpha}} \sqrt{\frac{Z^2 h^2}{\pi^2 a_0^2}} = \frac{\sqrt{2}}{\sqrt{\alpha}} \frac{Z h}{\pi a_0}$.

So, the equation becomes:

$\frac{6\pi a_0}{Z} = \frac{h}{\frac{\sqrt{2}}{\sqrt{\alpha}} \frac{Z h}{\pi a_0}}$.

$\frac{6\pi a_0}{Z} = \frac{h \sqrt{\alpha} \pi a_0}{\sqrt{2} Z h}$.

Cancel $h$ from the numerator and denominator on the right side:

$\frac{6\pi a_0}{Z} = \frac{\sqrt{\alpha} \pi a_0}{\sqrt{2} Z}$.

Cancel $\frac{\pi a_0}{Z}$ from both sides:

$6 = \frac{\sqrt{\alpha}}{\sqrt{2}}$.

Multiply both sides by $\sqrt{2}$:

$\sqrt{\alpha} = 6\sqrt{2}$.

Square both sides to find $\alpha$:

$\alpha = (6\sqrt{2})^2 = 6^2 \times (\sqrt{2})^2 = 36 \times 2 = 72$.

The value of $\alpha$ is 72.