Question
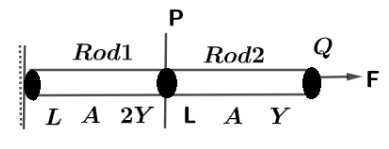
Question: Consider an arrangement shown in the diagram which is a combination of two rods \((1)\) and \((2)\) ...
Consider an arrangement shown in the diagram which is a combination of two rods (1) and (2) .Their length, cross sectional area and Young modulus are shown in the diagram. If force F is applied at the end of rod (2) .then total elongation of the combined system is (P is the common end of rods (1) and (2) ).
A. YA3FL
B. 2YAFL
C. 2YA3FL
D. YAFL
Solution
In order to solve the above problem, we will find the elongation in each rods separately due to applied force and then add their elongation to get a net increase in length of the system.
Formula used:
Young modulus of a material is given as,
Y=AFLΔL
where ΔL denotes for elongation of a material and A is the area of the cross section of given material.
Complete step by step answer:
Let us first find the ΔL for rod (1) ,
We have, Force =F
Young modulus =2Y
So, ΔL1=2AYFL→(i) Using the Young modulus formula.
Similarly, we will find the elongation for rod (2)
Young modulus =Y
So, ΔL for rod (2) is given by,
ΔL2=AYFL→(ii)
Now, add both equations (i)and(ii) we get,
Elongation=ΔL1+ΔL2
∴Elongation=2AY3FL
So, the net elongation of the combined system is Elongation=2AY3FL.
Hence, the correct option is C.
Note: Remember theoretically, Young modulus is defined as the ratio of stress (which is pressure acting on a material) to the strain (which is ratio of change in length of a body to its original length) and its SI unit is same as of Pressure Nm−2 . Also, in the given problem, Force was equally distributed along the line of two rods hence both rods were exerted by the same amount of force.
